
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Грина
|
|
|
|
.
Пример 2. Найти 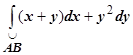 по кривой
по кривой 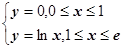 .
.
|
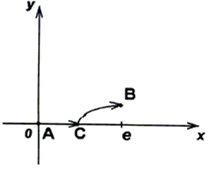
Решение: Пользуясь свойством аддитивности, разобьем интеграл на сумму двух:
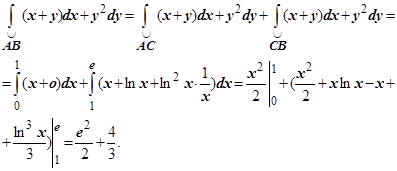
Пример 3. Найти 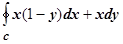 , где C - окружность, проходимая в отрицательном направлении (по часовой стрелке).
, где C - окружность, проходимая в отрицательном направлении (по часовой стрелке).
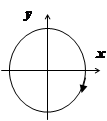 Решение: Параметризуем окружность x =2cos t, y =2sin t, 0 £ t £ 2p. Движению по часовой стрелке соответствует уменьшение параметра t, поэтому интегрируем от
Решение: Параметризуем окружность x =2cos t, y =2sin t, 0 £ t £ 2p. Движению по часовой стрелке соответствует уменьшение параметра t, поэтому интегрируем от 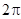 до 0:
до 0:
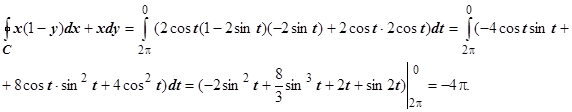 Пример 4. Вычислить
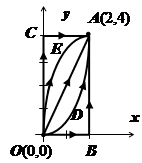
Пример 4. Вычислить 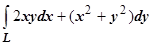 по каждому из путей, соединяющих точки О (0,0) и А (2,4), и изображённых на рисунке справа:
по каждому из путей, соединяющих точки О (0,0) и А (2,4), и изображённых на рисунке справа:
1. Ломаная ОВА, состоящая из прямолинейных отрезков;
2. Ломаная ОСА;
3. Прямолинейный отрезок ОА;
4-5. Параболы ODA и OEA, симметричные относительно координатных осей.
Решение. 1. 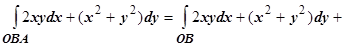
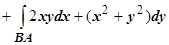 (по свойству аддитивности). На ОВ в качестве параметра естественно выбрать переменную х, при этом
(по свойству аддитивности). На ОВ в качестве параметра естественно выбрать переменную х, при этом 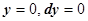 , поэтому
, поэтому 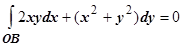 . На ВА
. На ВА 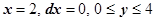 , поэтому
, поэтому  . Окончательно,
. Окончательно,  .
.
2. 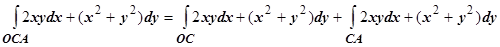 .
.
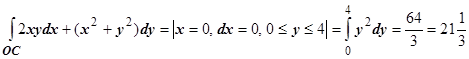 .
. 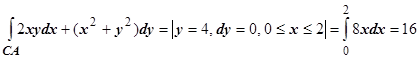 . Окончательно,
. Окончательно, 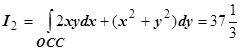 .
.
3. На прямолинейном отрезке ОА 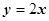 , поэтому
, поэтому  .
.
4. Уравнение параболы ОЕА имеет вид 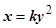 , значение коэффициента k найдём, подставляя в это уравнение координаты точки А:
, значение коэффициента k найдём, подставляя в это уравнение координаты точки А: 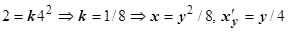 , поэтому
, поэтому 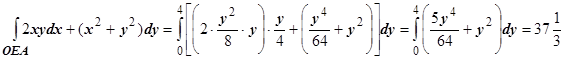 .
.
5. Совершенно также убеждаемся, что интеграл по параболе ODA имеет то же значение.
Закономерен вопрос: для любого ли интеграла и любых начальной и конечной точек значение интеграла не зависит от формы пути, соединяющего эти точки? Убедимся в том, что это не так, на примере интеграла 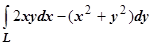 :
: 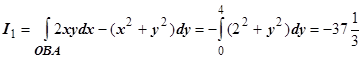 ;
; 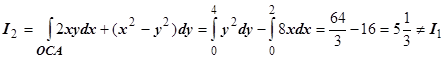 .
.
Следующие разделы будут посвящены ответу на поставленный вопрос: при каких условиях криволинейный интеграл второго рода 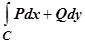 не зависит от формы пути, соединяющего начальную и конечную точки, и определяется только этими точками? В трёхмерном случае этот вопрос будет изучаться в теории поля.
не зависит от формы пути, соединяющего начальную и конечную точки, и определяется только этими точками? В трёхмерном случае этот вопрос будет изучаться в теории поля.
16.3.3.4.1. Связность, односвязность, многосвязность. Напомним определения ряда понятий из теории функций нескольких переменных, которыми нам придется пользоваться.
Множество точек (на прямой, на плоскости, в пространстве) называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
Область (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области.
Примеры: односвязны шар, параллелепипед и вообще любой выпуклый объём в пространстве. Односвязен шаровой слой, заключённый между двумя сферами. Пример неодносвязной области: тор. Все пространство односвязно и остаётся односвязным, если из него удалить точку или отрезок. Если же удалить из пространства прямую, оно потеряет свойство односвязности: окружность, охватывающую эту прямую, не удастся стянуть в точку, не пересекая прямую.
Кусочно-гладкая граница ограниченной односвязной области всегда связна, следовательно, является контуром.
16.3.3.4.2. Теорема Грина для односвязной области. Пусть на плоскости Oxy задана односвязная область D, ограниченная кусочно-гладким контуром C. На множестве 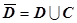 определены непрерывные функции
определены непрерывные функции 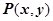 и
и 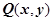 , имеющие непрерывные частные производные. Тогда
, имеющие непрерывные частные производные. Тогда 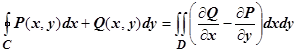 , при этом контур С обходится так, что область D остаётся слева.
, при этом контур С обходится так, что область D остаётся слева.
Док-во. 1. Пусть D - простая область. Докажем сначала, что 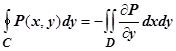 .
. 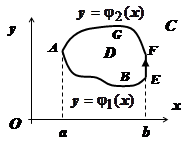 Опишем D неравенствами
Опишем D неравенствами 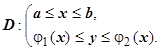 Тогда
Тогда 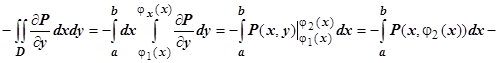
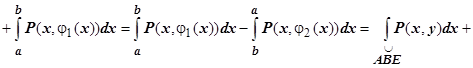
 . Если контур включает вертикальные участки, такие как EF, то на этих участках dx = 0, поэтому
. Если контур включает вертикальные участки, такие как EF, то на этих участках dx = 0, поэтому  , и
, и 
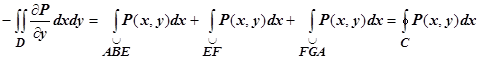 , что и требовалось доказать.
, что и требовалось доказать.
Равенство 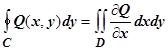 доказывается точно также:
доказывается точно также: 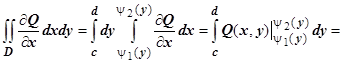
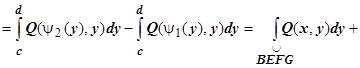
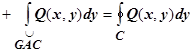 . Суммируя равенства
. Суммируя равенства 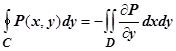 и
и 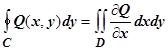 , получим одну из важнейших формул анализа -формулу Грина
, получим одну из важнейших формул анализа -формулу Грина
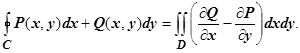
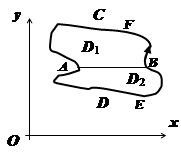 2. Пусть теперь D - произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком АВ, и пусть подобласти D 1 и D 2 - результат разбиения. Для этих подобластей формула Грина доказана:
2. Пусть теперь D - произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком АВ, и пусть подобласти D 1 и D 2 - результат разбиения. Для этих подобластей формула Грина доказана:
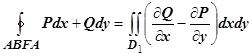 и
и 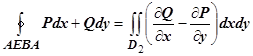 . По свойству аддитивности
. По свойству аддитивности 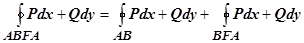 ,
, 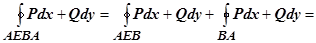
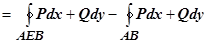 . Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.
. Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам АВ и ВА взаимно уничтожаются, а сумма интегралов по кривым ВFA и AEB даёт интеграл по контуру С, т.е. формула Грина верна и для области, не являющейся простой. Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.
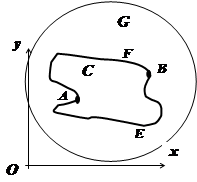
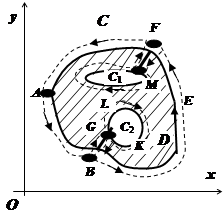 16.3.3.4.3. Теорема Грина для многосвязной области. Пусть теперь D многосвязная на плоскости Oxy. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек. Рассмотрим случай, когда граница области D (на рисунке область заштрихована) состоит из внешнего контура С и внутренних контуров С 1 и С 2. Соединим контур С разрезом FM с контуром С 1, разрезом BG - с контуром С 2. (Под словами "соединим разрезом BG " подразумевается то, что мы удалим из D отрезок BG). Область
16.3.3.4.3. Теорема Грина для многосвязной области. Пусть теперь D многосвязная на плоскости Oxy. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек. Рассмотрим случай, когда граница области D (на рисунке область заштрихована) состоит из внешнего контура С и внутренних контуров С 1 и С 2. Соединим контур С разрезом FM с контуром С 1, разрезом BG - с контуром С 2. (Под словами "соединим разрезом BG " подразумевается то, что мы удалим из D отрезок BG). Область 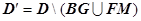 с границей
с границей 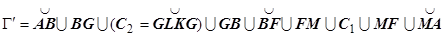 односвязна, поэтому для неё справедлива формула Грина:
односвязна, поэтому для неё справедлива формула Грина:
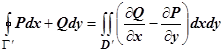 . Двойные интегралы по областям D и
. Двойные интегралы по областям D и 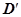 равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой
равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой  интегралы по разрезам входят с противоположными знаками (
интегралы по разрезам входят с противоположными знаками (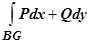 и
и 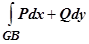 , например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей
, например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей 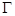 . На множестве
. На множестве  определены непрерывные функции
определены непрерывные функции 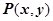 и
и 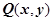 , имеющие непрерывные частные производные. Тогда
, имеющие непрерывные частные производные. Тогда 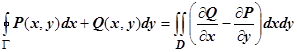 , при этом каждая часть полной границы
, при этом каждая часть полной границы 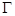 обходится так, что область D остаётся слева.
обходится так, что область D остаётся слева.
16.3.3.5. Условия независимости криволинейного интеграла от пути интегрирования. В этом разделе будет дан ответ на вопрос: при каких условиях криволинейный интеграл второго рода 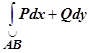 не зависит от формы пути, соединяющего точки А и В, а определяется только этими точками? Будем предполагать, что в некоторой односвязной области
не зависит от формы пути, соединяющего точки А и В, а определяется только этими точками? Будем предполагать, что в некоторой односвязной области 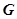 на плоскости заданы непрерывно дифференцируемые функции
на плоскости заданы непрерывно дифференцируемые функции 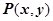 и
и 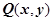 , и все рассматриваемые точки, контуры и области принадлежат этой области.
, и все рассматриваемые точки, контуры и области принадлежат этой области.
 16.3.3.5.1. Теорема 1. Для того, чтобы интеграл
16.3.3.5.1. Теорема 1. Для того, чтобы интеграл 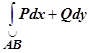 не зависел от формы пути, соединяющего точки А и В, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру был равен нулю.
не зависел от формы пути, соединяющего точки А и В, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру был равен нулю.
Доказательство. Необходимость. Пусть 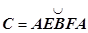 - произвольный замкнутый контур, лежащий в области
- произвольный замкнутый контур, лежащий в области 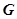 , А и В - произвольные точки этого контура. Так как, по условию,
, А и В - произвольные точки этого контура. Так как, по условию, 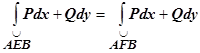 , то
, то 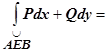
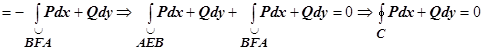 .
.
Достаточность. Пусть для любого контура 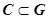 выполняется
выполняется 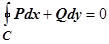 . Пусть
. Пусть 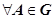 ,
, 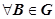 - произвольные точки,
- произвольные точки, 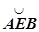 и
и 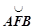 - две различных кривых, соединяющих эти точки.
- две различных кривых, соединяющих эти точки. 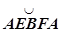 - замкнутый контур, поэтому
- замкнутый контур, поэтому 

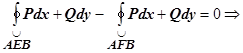
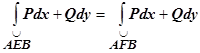 , что и требовалось доказать.
, что и требовалось доказать.
16.3.3.5.2. Теорема 2. Для того, чтобы интеграл 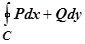 по любому контуру С был равен нулю, необходимо и достаточно, чтобы функции
по любому контуру С был равен нулю, необходимо и достаточно, чтобы функции 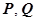 и их частные производные были непрерывны, и выполнялось условие
и их частные производные были непрерывны, и выполнялось условие 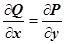 .
.
Доказательство. Необходимость. От противного. Пусть для 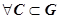 выполняется
выполняется 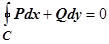 , но существует точка
, но существует точка  такая, что
такая, что 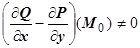 . Предположим для определённости, что
. Предположим для определённости, что 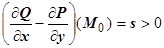 . Так как разность
. Так как разность 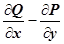 непрерывна, существует окрестность точки
непрерывна, существует окрестность точки 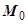 такая, что
такая, что 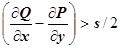 . Выберем контур С, целиком лежащий в этой окрестности. Если D - область ограниченная этим контуром, то, по формуле Грина,
. Выберем контур С, целиком лежащий в этой окрестности. Если D - область ограниченная этим контуром, то, по формуле Грина, 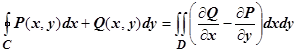 . Но, по теореме об интегрировании неравенств,
. Но, по теореме об интегрировании неравенств, 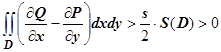 (
(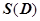 - площадь области D), т.е.
- площадь области D), т.е. 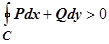 , что противоречит условиям теоремы. Следовательно, в любой точке
, что противоречит условиям теоремы. Следовательно, в любой точке  выполняется условие
выполняется условие 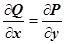 .
.
Достаточность. Если в любой точке  выполняется условие
выполняется условие 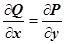 , то для любого контура С
, то для любого контура С 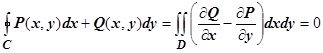 (D - область ограниченная контуром С).
(D - область ограниченная контуром С).
Таким образом, для того, чтобы криволинейный интеграл 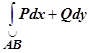 не зависел от формы пути, соединяющего начальную и конечную точки (или, что то же самое, интеграл по любому замкнутому контуру был равен нулю), требуется выполнение двух условий:
не зависел от формы пути, соединяющего начальную и конечную точки (или, что то же самое, интеграл по любому замкнутому контуру был равен нулю), требуется выполнение двух условий:
1. Контур и ограниченная им область лежат в некоторой односвязной области, в которой
2. 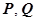 и их частные производные непрерывны, и
и их частные производные непрерывны, и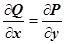 .
.
Отметим существенность первого условия. Так, для интеграла 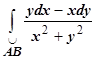 второе условие выполняется:
второе условие выполняется: 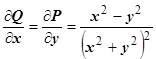 , в то же время интеграл по окружности радиуса R не равен нулю:
, в то же время интеграл по окружности радиуса R не равен нулю: 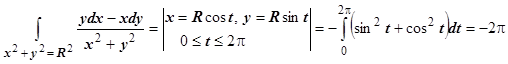 . Причина - функции Р и Q непрерывны всюду, кроме начала координат; удаление точки из плоскости лишает её свойства односвязности.
. Причина - функции Р и Q непрерывны всюду, кроме начала координат; удаление точки из плоскости лишает её свойства односвязности.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 901; Нарушение авторских прав?; Мы поможем в написании вашей работы!