Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути

Если выполнены условия независимости от формы пути, соединяющего начальную 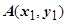и конечную 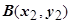точки кривой, то значение интеграла 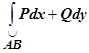определяется только точками А и В. Поэтому в этом случае для обозначения интеграла применяется обозначение 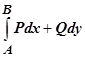или . Докажем следующую теорему.

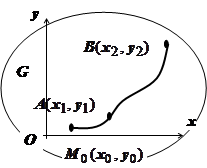Теорема. Если в односвязной области G выполнено условие 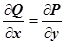, то существует функция 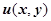такая, что для любых точек и .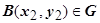

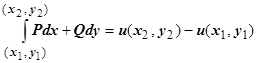Функцию 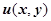принято называть потенциальной функцией.

Доказательство. Фиксируем произвольную точку , и докажем, что в качестве искомой функции 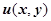можно взять 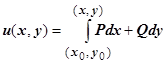. Действительно, по свойству аддитивности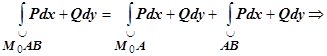 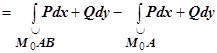, или , т.е. 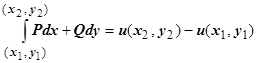, что и требовалось доказать.

Разность 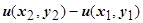обозначается символом или 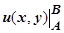. Формула является аналогом формулы Ньютона-Лейбница для двухмерного случая; ещё раз отметим, что она имеет место в случае, когда выполняются условия независимости интеграла от формы пути.

Докажем, что для построенной функции 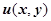выполняются следующие соотношения:

. Действительно, пусть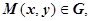

. Тогда ,

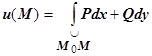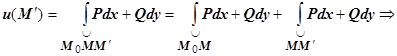
(на ) 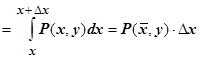(по теореме о среднем) . Точка удовлетворяет условиям . Устремим 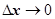, тогда 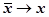, и .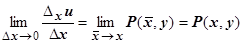

Аналогично доказывается, что .

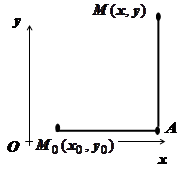Условие 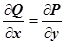теперь означает просто, что 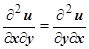. Кроме того, из 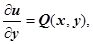следует, что подынтегральное выражение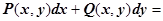 является полным дифференциалом функции 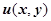(условие 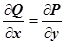есть условие того, что обыкновенное дифференциальное уравнение первого порядка 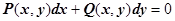- уравнение в полных дифференциалах). Для отыскания потенциальной функции 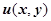можно: 1. Решить уравнение в полных дифференциалах; 2. Построить 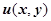напрямую по формуле 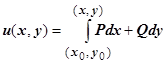. В качестве пути интегрирования обычно берётся путь М ₀ АМ, состоящий из отрезков, параллельных координатным осям.

Тогда на М ₀ А 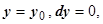; на АМ .

Продемонстрируем оба метода на примере 4 раздела 16.3.3.3: 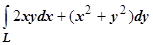. Здесь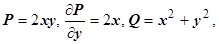 , т.е. условия независимости выполняются. В качестве точки 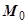берём начало координат .

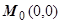1. Решаем систему уравнений 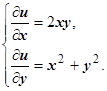Из первого уравнения 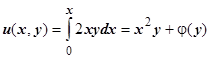, подставляем эту функцию во второе уравнение (потенциал всегда определяется с точностью до произвольной постоянной, физический смысл имеет разность потенциалов в двух точках, которая не зависит от этой постоянной).

2. .

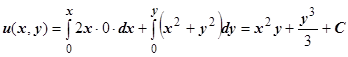Теперь, когда потенциальная функция определена, легко находится любой интеграл: .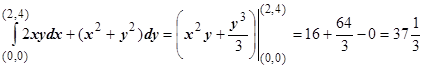

16.3.3.7. Выражение площади плоской области через криволинейный интеграл. Из формулы Грина 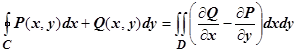следует неожиданный результат: если функции Р и Q удовлетворяют условию 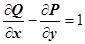, то 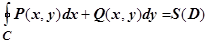(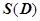- площадь области D). Таким образом, площадь области можно выразить через криволинейный интеграл второго рода по границе этой области. В качестве функций Р и Q можно взять любые непрерывно дифференцируемые функции, такие что 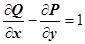, например, 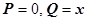; ; 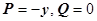; 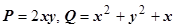и т.д. В результате 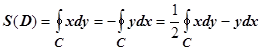и т.д. При этом контур С (граница области D) обходится в положительном направлении. Чаще всего применяется третья из этих формул. Для примера найдём площадь, ограниченную эллипсом 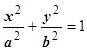. Параметрические уравнения эллипса , поэтому 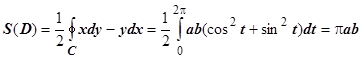; это, видимо, самый простой способ вычисления площади эллиптической области.

16.4. Поверхностные интегралы.

16.4.1. Односторонние и двусторонние поверхности. Ориентация поверхности. Поверхность может быть односторонней и двусторонней. Простой пример модели односторонней поверхности - лист Мёбиуса, который получается, если взять узкую длинную полоску бумаги и склеить её узкие торцы, перекрутив полоску один раз. В том, что у полученной поверхности одна сторона, можно убедиться, если начать закрашивать её в какой-нибудь цвет, не отрывая кисть от бумаги и не пересекая границ. В результате будет окрашен весь лист Мёбиуса. Мы будем рассматривать только двусторонние поверхности.

Поверхность называется гладкой, если в каждой её точке существует касательная плоскость, непрерывно меняющаяся вдоль поверхности. Поверхность называется кусочно-гладкой, если она состоит из нескольких гладких частей, примыкающим друг к другу по гладким или кусочно- гладким кривым. Так, плоскость - гладкая поверхность; поверхность куба - кусочно-гладка.

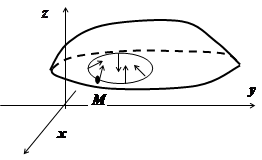Дадим формальное определение односторонней и двусторонней поверхностей. Пусть дана гладкая поверхность 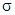, и на ней произвольно выбрана точка М. Из двух возможных направлений нормали в этой точке выберем одно и зафиксируем его. Характеризовать это направление будем единичным вектором нормали 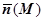. Возьмём замкнутый контур С, проходящий через точку М, целиком лежащий в 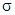и не пересекающий её границы, и будем двигаться по контуру, восстанавливая в каждой точке нормаль так, чтобы она непрерывно получалось из 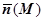. Если для любого такого контура и любой точки М мы вернёмся в М с исходным направлением нормали, то поверхность 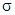называется двусторонней. Если хотя бы для одного контура мы вернёмся в исходную точку с противоположным направлением нормали, то поверхность называется односторонней.

Задать ориентацию поверхности (выбрать определённую сторону поверхности) означает выбрать в каждой точке 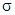один из двух возможных векторов нормали 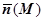так, чтобы он непрерывно менялся от точки к точке. Для этого достаточно определить нормаль в какой-либо одной точке 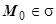; во всех остальных точках М направления нормали 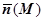должны браться так, чтобы они получались непрерывным переносом из 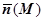вдоль какого-нибудь пути . Согласно определению двусторонней поверхности, мы гарантированно придём в точку с одним и тем же направлением нормали при любом пути .

16.4.2. Поток жидкости через поверхность. Как и при изучении криволинейных интегралов, начнём с физической задачи. Пусть через объём V течёт поток жидкости, имеющий скорость в точке М. Пусть в V размещена проницаемая (возможно, воображаемая) поверхность 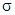. Требуется найти количество 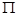жидкости, протекающей через 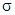за единицу времени. В дальнейшем мы будем называть это количество потоком через поверхность.

В случае, когда 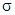- ограниченная плоская область и , решение очевидно. Это количество равно объёму, ограниченному цилиндрической поверхностью с основанием 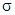и боковой стороной . Площадь основания объёма равна 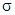(этим символом мы обозначаем и поверхность, и её площадь), высота 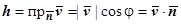, т.е. равна скалярному произведению вектора скорости на единичный вектор нормали. Итак, . Заметим, что изобразив на рисунке единичный вектор нормали, мы ввели на поверхности ориентацию. Так, применительно к рисунку справа, мы выбрали верхнюю сторону поверхности; если бы выбрали противоположную нормаль, поток изменил бы знак.

Возможны два способа представления этой величины.

1. Обозначив 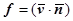, получим .

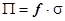2. Если в некоторой координатной системе 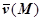имеет координаты P, Q, R, единичный вектор 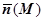имеет координаты - направляющие косинусы , то . Чему равно произведение ? Произведение 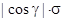равно площади 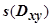проекции поверхности 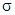на

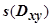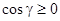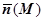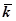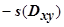плоскость Oxy (площади всегда положительны). Следовательно, равно , если (или, что то же самое, угол - острый; проекция на орт оси Oz положительна). Этот случай соответствует верхнему рисунка справа. Соответственно, равно , если 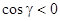(или, что то же самое, угол - тупой; проекция 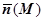на орт 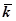оси Oz отрицательна). Этот случай соответствует нижнему рисунку. Итак, можно записать 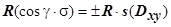. 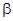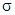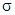Аналогично изложенному, , где следует взять знак "+", если угол - острый, и "-", если этот угол тупой, и , где берётся знак "+", если угол - острый, и "-", если этот угол тупой; - проекция на плоскость Oyz, - - проекция на плоскость Oxz. Окончательно, .

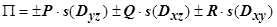Пусть теперь 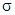- произвольная гладкая ограниченная поверхность, и скорость может меняться от точки к точке. Чтобы свести этот случай к предыдущему, разобьём 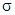сетью кривых на 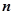частей 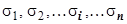, на каждой из частей выберем произвольную точку 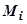, и, считая, что - плоская область, скорость по постоянна и равна и что ориентация всей части характеризуется единичным нормальным вектором 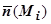, получим, что через в единицу времени протекает жидкости (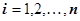). Как мы видели, это выражение можно представить и в виде (где 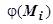- угол между 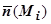и ), и в виде 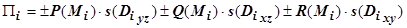. Суммируя эти выражения по всем 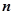дугам, получим выражения двух интегральных сумм: 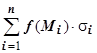и 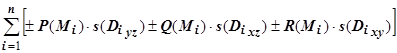. Переход к пределу в этих интегральных суммах при приведёт к двум поверхностным интегралам: и 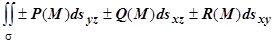. Первый из этих интегралов называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности. Во втором интеграле элементы площади в координатных плоскостям принято записывать так, как мы это делали в двойном интеграле: и опускать знаки перед слагаемыми: 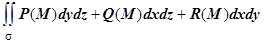; этот интеграл называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам. Как и криволинейные интегралы двух родов, это разные объекты. Они имеют разные определения и разные свойства. В частности, поверхностный интеграл первого рода не зависит от ориентации поверхности, так как угол 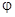входит в подынтегральную функцию в явном виде, в то время как поверхностный интеграл второго рода меняет знак при изменении стороны поверхности (вектор 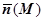меняется на ).

Перейдём к формальным определениям.

Дата добавления: 2014-01-07