Основные понятия механики сплошных сред для биологических жидкостей

Биомеханика крови

Раздел биомеханики крови имеет название «реология крови».

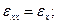
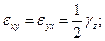
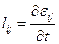
Также, как и в теории упругих сред, в теории жидких сред вводят линейные и угловые деформации.

Линейная деформация – относительное изменение размеров.

Угловые деформации: Сдвиг деформации обозначается с несимметричными индексами , причем сдвиг деформации определяют как углы поворота вокруг дополнительных осей.

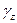- угол поворота при сдвиговой деформации

Вводят понятие скорости деформации

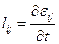
Удвоенную скорость деформации по модулю называют скоростью сдвига, для неё имеется специальное обозначение

Уравнение, которое описывает связь сдвиговых напряжений в жидкой среде:

- основное реологическое уравнение жидких сред.

- коэффициент вязкости [Па*с]

- напряжение сдвига [Па]

- скорость сдвига [1/c]

Эквивалентная запись:

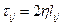
Уравнение Ньютона

В зависимости от того, является ли в уравнении постоянным или является функцией скорости сдвига 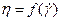, все жидкие среды принято классифицировать на два больших класса:

1) 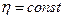Ньютоновская жидкость;

2) 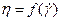Неньютоновская жидкость. Для всех жидких сред зависит только от скорости сдвига (если течение стационарное).

Для большинства биологических жидкостей экспериментально получены зависимости от скорости сдвига, в частности это можно проиллюстрировать следующими графиками

При больших скоростях сдвига зависимость приблизительно линейная, близкая к ньютоновской жидкости.

Для крови наиболее общепринятой экспериментальной зависимостью, описывающую связь и , является модель Кессона.

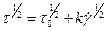- эмпирическая модель, описывающая поведение кривой.

Любые модели должны не противоречить модели Кессона.

Сплошная среда связана с градиентами скоростей в стационарном потоке.

Поле скоростей связано с взаимодействием текущих слоев, составом среды, свойствами среды.

Дата добавления: 2014-01-07