Лекция 3. Практическая реализация графического метода решения задач линейного программирования

План

1. Пример графического решения задачи ЛП.

2. Задачи ЛП, сводящиеся к графическому методу решения.

3. Решение задач линейного целочисленного программирования графическим методом.

1. Рассмотрим графическое решение конкретной задачи ЛП.

Пример 1. Решить графически задачу ЛП:

Z = 4 x 1 + 2 x 2 → max,

⎪

⎧− x 1

⎪ 2 x 1

⎨

+ 3 x 2 ≤ 9

+ 3 x 2 ≤18

⎪ −2 x 1 + x 2 ≥ −10

2 x 1 − x 2 ≥ 0

x 1 ≥ 0, x 2 ≥ 0.

Решение. Для нахождения ОДР строим граничные прямые и определяем

полуплоскости, координаты точек которых удовлетворяют ограничениям.

Рассмотрим первое ограничение

− x 1 + 3 x 2 ≤ 9. Строим прямую

l 1:

− x 1 + 3 x 2 = 9

по двум точкам

x 1 = 0,

x 2 = 3 и

x 1 = −9,

x 2 = 0. Берём контроль-

ную точку, не лежащую на этой прямой, например,

O (0; 0). Подставляем её ко-

ординаты в первое ограничение. Если неравенство в этой точке выполняется, то первое ограничение определяет полуплоскость, которая содержит контрольную точку, если же нет, то оно определяет полуплоскость, в которой не лежит кон-

трольная точка. В точке

O (0; 0)

неравенство выполняется:

−0 + 3 ⋅ 0 = 0 < 9. По-

этому первое ограничение определяет полуплоскость, расположенную ниже прямой l 1. На рис. 1 это отмечено двумя стрелками.

Аналогично поступаем с остальными тремя ограничениями. Результаты вычислений запишем в табл. 1.

Табл. 1. Вспомогательные расчёты

Пря- мая	Уравнение прямой	Точки на прямых	Кон- троль- ная точка	Знак нера- венства в этой точке	Принадлеж- ность кон- трольной точки к ОДР
l 1 l 2 l 3 l 4	− x 1 + 3 x 2 = 9 2 x 1 + 3 x 2 = 18 −2 x 1 + x 2 = −10 2 x 1 − x 2 = 0	(0,3) (–9,0) (0,6) (9,0) (0,–10) (5,0) (0,0) (1,2)	О(0,0) О(0,0) О(0,0) М(0,5)	–0+3⋅0 <9 2⋅0+3⋅0 <18 –2⋅0+0 >–10 2⋅0–5<0	О принадлежит О принадлежит О принадлежит М не принадл.

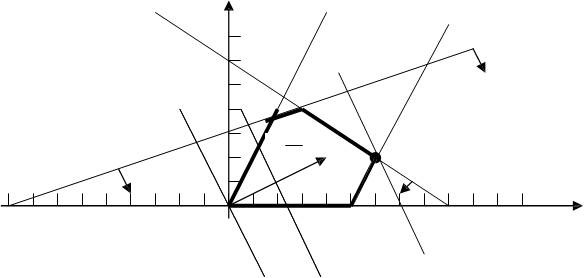
Выделяем ОДР – пятиугольник OABCD. Строим вектор

G

c = (4, 2), пока-

зывающий направление наибольшего возрастания функции Z. Строим изоцель

– прямую, перпендикулярную вектору c:

4 x 1 + 2 x 2 = 0.

Т.к. мы ищем максимум целевой функции, то изоцель следует переме-

щать параллельными переносами в направлении вектора c, пока она не станет

опорной к ОДР (рис. 1). Это произойдёт в точке

точки C:

C (x 1; x 2). Находим координаты

⎧ l 2, ⇒

⎧2 x 1 + 3 x 2 =18, ⇒

⎧ x 1 = 6,

⎨ ⎨ ⎨

⎩ l 3,

⎩2 x 1 −

x 2 =10,

⎩ x 2 = 2.

l 2 x 2 l 4 l 3

А

B

l 1 c

C (6,2)

x 1

0 D

Рис. 1. Иллюстрация графического метода

Найдено единственное оптимальное решение

чение целевой функции:

X * = (6; 2). Вычисляем зна-

Ответ:

X * = (6; 2),

Z max

Z max

= Z (X *) = 4 ⋅ 6 + 2 ⋅ 2 = 28.

= 28.

Заметим, что в точке

O (0; 0)

достигается минимум целевой функции, рав-

ный

Z min

= 0.

2. Мы научились применять графический метод для задач ЛП, которые содер-

жат две переменные

x 1 и

x 2.

На самом деле, некоторые задачи ЛП, размерность которых превышает 2, можно свести к задаче двух переменных. Остальные переменные при этом должны быть исключены.

Пример 2. Решить задачу ЛП:

Z = −16 x 1− x 2 + x 3 + 5 x 4 + 5 x 5 → max,

⎨ 1 2

⎧2 x 1+ x 2 + x 3

⎪−2 x + 3 x

+ x 4

=10

= 6

⎩ 1 2

⎪2 x + 4 x

− x 5 = 8

x j ≥ 0 (j =1, 5).

Решение. Выразим неизвестные

x 3, x 4, x 5

из первого, второго и третьего

равенств системы ограничений соответственно:

⎧ x 3 =10 − 2 x 1 − x 2

⎪

⎩ 5 1 2

⎨ x 4 = 6 + 2 x 1 − 3 x 2

⎪ x = −8 + 2 x + 4 x

Исключаем данные неизвестные из целевой функции:

/

(1)

Z = −16 x 1− x 2 + (10 − 2 x 1 − x 2) + 5(6 + 2 x 1 − 3 x 2) + 5(−8 + 2 x 1 + 4 x 2) = 2 x 1 + 3 x 2.

Т.к. все переменные задачи – неотрицательные, то предыдущую систему ра-

венств запишем в виде системы неравенств:

⎧10− 2 x 1 − x 2 ≥ 0

⎪

⎨6 + 2 x 1 − 3 x 2 ≥ 0

⎧2 x 1 + x 2 ≤10

⎨ 1 2

⎪−2 x + 3 x ≤ 6

⎪−8+ 2 x + 4 x ≥ 0

⎪2 x

+ 4 x ≥ 8

⎩

Получена задача ЛП:

⎩ 1 2

1 2

/

Z = 2 x 1 + 3 x 2 → max,

⎨ 1 2

⎧2 x 1 + x 2 ≤10

⎩ 1 2

⎪−2 x + 3 x ≤ 6

⎪2 x + 4 x ≥ 8

x 1 ≥ 0, x 2 ≥ 0.

Решим её графическим методом.

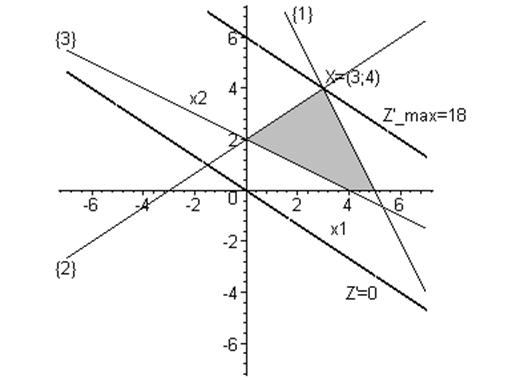
Для данной задачи ОДР – заштрихованный четырёхугольник ABCD (рис.

2). Уравнение изоцели следующее:

2 x 1 + 3 x 2 = 0.

ДвиGгая изоцель параллельными переносами в направлении градиент-

вектора

c = (2,3), достигнем опорной точки

C (x 1; x 2). Эта точка находится на

пересечении прямых I и II:

⎧2 x 1 + x 2 =10

⎩ 1 2

⎨−2 x + 3 x = 6

⎧ x 1 = 3

= 4

⎨

⎩ x 2

/

При этом

Z max

=18.

Осуществим обратную замену, подставив координаты точки систему (1):

C (3; 4) в

⎧ x 3 = 0

⎪

⎩ 5

⎨ x 4 = 0

 

⎪ x =14

Рис. 2. Графическое решение примера 2

Получено единственное оптимальное решение исходной задачи ЛП

X * = (3; 4; 0; 0;14). Подставив его в целевую функцию, убедимся в том, что

Z max

= Z (X *) = −16 ⋅ 3 − 4 + 0 + 5 ⋅ 0 + 5 ⋅14 =18.

Ответ:

X * = (3; 4; 0; 0;14),

Z max

=18.

3. Рассмотрим возможности графического метода при решении задач линейно-

го целочисленного программирования.

Пример 3. Дана задача:

Z = 2 x 1 + 3 x 2 → max,

⎧ x 1

⎨

+ 2 x 2 ≤ 6

⎩ 8 x 1

+ 7 x 2 ≤ 28

x 1 ≥ 0, x 2 ≥ 0,

x 1, x 2 ∈ ].

Требуется: 1) решить графическим методом задачу ЛП без учёта целочисленно-

сти; 2) решить ту же задачу с условием целочисленности.

Решение. 1) Для задачи ЛП имеем ОДР – четырёхугольник OABC, с уг-

ловыми точками

O (0; 0),

A (0;3),

B (14 / 9; 20 / 9),

C (7 / 2; 0). Наибольшее значе-

ние целевой функции достигается в точке B, поэтому имеем оптимальное ре-

шение

X = (14 / 9; 20 / 9),

Z (X) = 88 / 9 = 9 7

(рис. 3).

Найденное решение не является целочисленным. Будем искать оптималь-

ную точку с целочисленными координатами.

2) Отметим в ОДР точки с целочисленными координатами, близко распо-

ложенные к границе или лежащие на границе, участок которой содержит точку

X = (14 / 9; 20 / 9)

(рис. 3). Такими точками являются (0;3), (1; 2), (2;1), (3; 0).

Вычисляем в этих точках значения целевой функции

Z (0;3) = 9,

Z (1; 2) = 8,

Z (2;1) = 7,

Z (3; 0) = 6, и выбираем из них наибольшее.

Оптимальное целочисленное решение

X * = (0;3),

Z (X *) = 9.

Рис. 3. Графическое решение примера 3

Лекция 4. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ СИМПЛЕКС-

Дата добавления: 2014-01-07