Лекция 8. Метод искусственного базиса решения задач линейной оптимизации

1. Метод искусственного базиса.

План

2. Пример решения задачи ЛП методом искусственного базиса.

1. При решении задач ЛП симплекс-методом предполагалось, что среди векто-

ров

A 1,

A 2,...,

A j,..., An

имеется m единичных векторов. Т.е. в каждом уравне-

нии есть базисная переменная, которая входит лишь в одно уравнение с коэф-

фициентом 1, а в остальные – с коэффициентом 0.

Рассмотрим исходную задачу в каноническом виде:

Z = c 1 x 1 + c 2 x 2 + ⋅⋅⋅ + cnxn → min;

⎧ a 11 x 1 + a 12 x 2 + ⋅⋅⋅ + a 1 nxn = b 1,

⎨

⎩ m 1 1 m 2 2 mn n m

⎪ .................................................,

⎪ a x + a x + ⋅⋅⋅ + a x = b,

(1)

x j ≥ 0 (j =1 ,n).

Составляем расширенную задачу формальным добавлением новых базис-

ных (искусственных) переменных в уравнения, в которых их нет. В целевую функцию дописываем их с большим положительным числом M. Получим

расширенную задачу:

Z ′ = c 1 x 1

+ c 2 x 2 + ⋅⋅⋅ + cnxn + Мxn +1+ Мxn +2+ ⋅⋅⋅ + Мxn + m → min;

⎧ a 11 x 1 + a 12 x 2 + ⋅⋅⋅ + a 1 n xn +

xn +1

= b 1,

⎨

⎪ ...................................................................................................,

(2)

⎩ m 1 1 m 2 2 mn n

⎪ a x + a x + ⋅⋅⋅ + a x

+ xn + m = bm,

x j ≥ 0 (j =1 ,n + m), bi ≥ 0 (i =1 ,m).

Такой подход называют методом искусственного базиса. Ясно, что ис-

кусственные переменные должны равняться нулю. Если среди них имеются не равные нулю, то исходная задача (1) несовместная. Или, по-другому, целевая

функция расширенной задачи (2) будет неограниченно расти с ростом M и не сможет достичь минимума. Если в оптимальном плане расширенной задачи ис- кусственные переменные равны нулю, то остальные переменные дают решение

исходной задачи, если же есть не равные нулю, то исходная задача несовмест- ная. Если же на некотором этапе, после выведения искусственных переменных из базиса, возникнет столбец с неположительными членами и положительной

оценкой для данного столбца, то

Z → −∞. Если в оптимальном плане есть сво-

бодный вектор с нулевой оценкой, то оптимальный план не единственный.

2. Рассмотрим решение конкретной задачи ЛП с помощью метода искусствен-

ного базиса.

Пример 2. Решить задачу ЛП:

Z = x 1 + 2 x 2 + 2 x 3 → max;

⎧− x 1 + 2 x 2 − x 3 ≤ - 1,

⎪

⎨ x 1 + 2 x 2

≤1,

⎩

⎪ x 1 + 2 x 2 + x 3

= 3,

x j ≥ 0 (j =1, 3).

Решение. Переходим к канонической форме. Для этого делаем замену

Z′ = −Z. В первое и второе ограничения дописываем балансовые переменные

x 4,

x 5 и первое ограничение умножаем на (–1):

Z ′ = − x 1 − 2 x 2 − 2 x 3 + 0 x 4 + 0 x 5 → min;

⎧ x 1 − 2 x 2 + x 3

⎪

⎨ x 1 + 2 x 2

- x 4

+ x 5

=1,

=1,

⎩ 1 2

⎪ x + 2 x

+ x 3

= 3,

x j ≥ 0 (j =1, 5).

В первое и третье уравнение прибавляем, соответственно, искусственные

переменные

x 6,

x 7 с коэффициентом равным единице. В целевую функцию их

дописываем с коэффициентом M. Получили расширенную задачу:

Z ′′ = − x 1 − 2 x 2 − 2 x 3 + 0 x 4 + 0 x 5 + Мx 6 + Mx 7 → min;

⎧ x 1 − 2 x 2 + x 3 - x 4 +

⎪

[ x 6 ]

=1,

⎩ 1 2 3

⎨ x 1 + 2 x 2 +

⎪ x + 2 x + x +

[ x 5]

=1,

[ x 7 ] = 3,

x j ≥ 0 (j =1, 7).

Задачу решаем симплекс-методом (табл. 1).

Табл. 1. Первая симплекс-таблица с комментариями

Б 1	С Б	В 1	À 1	À 2	À 3	À 4	À 5	À 6	À 7
-1	-2	-2			М	М
À 6	М			-2	[1]	-1
À 5 À 7	М
z j − c j					-1

↓

θ

← 1/1 -1 -2

⎯

3/1

Имеем начальный опорный план

X Б 1 = (0, 0, 0, 0, 1, 1, 3)

при

Z ′′ (X Б 1 ) = −1⋅0 −2⋅0 −2⋅0 +0⋅0 +0⋅1+ М ⋅1+ М ⋅3 =0 +4 М = 4 М.

⎛ a ⎞

Числа в индексной строке имеют вид a + bM

и их записывают в виде

b

⎜ ⎟. Поэтому индексную строку записывают в двух уровнях. В (m +1) -ю стро-

⎝ ⎠

ку вносят a, а в (m + 2) -ю строку записывают b. Знак числа a + bM

⎛ 25 ⎞

совпадает

⎛0 ⎞

со знаком числа b, если

b ≠ 0. Например,

25 − 6 M

= ⎜ ⎟ < 0,

⎝ −6 ⎠

⎜ ⎟ > 0,

⎝1 ⎠

⎛ −6 ⎞

⎛ 0 ⎞

−6 + M

= ⎜ ⎟ > 0, ⎜ −1⎟< 0.

⎝ 1 ⎠ ⎝ ⎠

Сначала направляющий столбец выбирают по нижней строке, а после превращения искусственных переменных в свободные оптимизация произво- дится по верхней индексной строке.

Покажем, как находится индексная строка:

Z ′′

(X) =1⋅ М +1⋅ 0 + 3⋅ М = 0 + 4 М = ⎛0⎞,

⎝ ⎠

Б 1 ⎜ ⎟

⎛1⎞

z 1 − c 1 = 1 ⋅ M + 1 ⋅ 0 + 1 ⋅ M + 1 = 1 + 2 M = ⎜ ⎟,

⎝ ⎠

z 2 − c 2 = −2 ⋅ M + 2 ⋅ 0 + 2 ⋅ M + 2 = 2 + 0 ⋅ M

⎛ 2 ⎞

= ⎜ ⎟,

⎝ ⎠

⎛ 2 ⎞

z 3 − c 3 = 1⋅ M + 0 ⋅ 0 + 1⋅ M + 2 = 2 + 2 M

= ⎜ ⎟.

⎝ ⎠

Первый план не оптимален. В нижней индексной строке наибольшую

оценку имеют

À 1 и

À 3, Выбираем

À 3, т.к.

⎛ 2 ⎞ ⎛ 1 ⎞

⎜ ⎟ > ⎜ ⎟.

⎝ 2 ⎠ ⎝ 2 ⎠

Этот вектор вводим в базис.

⎨ ⎬

Вычисляем симплексное отношение:

θ03

= min ⎧1, = 3 ⎫ =1.

⎩1 1 ⎭

Выводим из базиса вектор

À 6. Составляем табл. 2.

Табл. 2 не содержит комментариев, позволяющих перейти к табл. 3. Под-

разумевается, что направляющая третья строка умножится на 1

и будет при-

бавлена к первой строке, на

⎛ − = 1 ⎞

и прибавлена ко второй, на

⎛ − = 3 ⎞

и прибав-

⎜ 2 ⎟

⎜ 2 ⎟

⎝ ⎠ ⎝ ⎠

лена к четвёртой, на (−1)

и прибавлена к пятой. В конце сама направляющая

третья строка будет умножена на 1.

θ

Табл. 2. Вторая симплекс-таблица с комментариями

Б 2	С	В 2	А 1	À 2	À 3	À 4	À 5	À 6	À 7
-1	-2	-2			М	М
À 3 À 5	-2			-2		-1
À 7	М			[4]				-1
z j − c j	-2	-1					-2 -2

↓

Б

2

⎯

1/2

← 1/2

Далее совершаем итерации до тех пор, пока не получим отрицательные оценки в индексной строке. Все вычисления отражены в табл. 3 и табл. 4. Ком- ментарии к вычислениям не записаны (студентам проделать самостоятельно).

Табл. 3. Третья симплекс-таблица с комментариями

Б 3	С Б	В 3	À 1	À 2	À 3	À 4	À 5	À 6	À 7
-1	-2	-2			М	М
À 3 À 5	-2					-1/2   -1/2		1/2   1/2	1/2   -1/2
À 2	-2	1/2				[1/4]		-1/4	1/4
z j − c j	-5	-1			1/2		-1/2 -1	-3/2 -1

↓

θ

⎯

⎯

← 2

Табл. 4. Четвёртая симплекс-таблица с комментариями

Б 4	С Б	В 4	À 1	À 2	À 3	À 4	À 5	À 6	À 7
-1	-2	-2			М	М
À 3 À 5 À 4	-2							-1
z j − c j	-6	-1	-2				-1	-2 -1

Делаем вывод о том, что

X opt

= (0;0;3;2;1;0;0),

Z m′in = −6. Все искусствен-

ные переменные равны нулю, поэтому начальные переменные определяют оп-

тимальный план.

∗

Ответ:

Х = (0;0;3),

Z max = 6.

Лекция 9. ТРАНСПОРТНАЯ ЗАДАЧА

План

1. Математическая модель транспортной задачи.

2. Методы построения начального опорного плана транспортной задачи.

1. Рассмотрим следующую задачу ЛП.

Пусть в регионе имеется m поставщиков угля (шахт) с запасами

a 1,

a 2,…,

am. В угле нуждаются n потребителей (тепловых электростанций) с по-

требностями

b 1,

b 2,…,

bn. Пусть

cij

(i =1, m,

j =1, n) – цена перевозки единицы

товара (например, за 1 т) от i -го поставщика j -му потребителю.

Требуется определить неизвестные величины

xij

(i =1, m,

j =1, n), обо-

значающие объём планируемой перевозки от i -го поставщика j -му потребите- лю. Будем стремиться минимизировать общую стоимость перевозок. Задачи та- кого типа называют транспортными задачами. Описанная задача однотовар-

ная.

Если выполняется условие

m n

∑ ai = ∑ bj, то совокупные запасы поставщи-

i =1

j =1

ков совпадают с совокупными потребностями. Тогда это закрытая транспорт-

ная задача. В противном случае – открытая (с нарушенным балансом).

Решение открытой задачи сводится к закрытой. Поэтому сформулируем

математическую модель закрытой транспортной задачи.

Пусть Z – общая стоимость перевозок. Тогда мы ищем минимум целевой функции:

m n

Z = c 11 x 11 + c 12 x 12 +...+ cmn xmn = ∑∑ cij xij → min. (1)

Запишем ограничения задачи:

⎪ x 21 22 2 n 2

⎧ x 11 + x 12 +...+ x 1 n = a 1

⎪ + x +...+ x = a

⎪ xm 1 m 2 mn m

⎪................................

⎪ x 11 21 m 1 1

⎪ + x +...+ x = a

⎨ + x +...+ x = b

⎪ x 12 + x 22 +...+ xm 2 = b 2

⎪

⎩

⎪................................

⎪ x 1 n + x 2 n +...+ xmn = bn

i =1

j =1

(2)

Объёмы перевозок должны быть неотрицательными:

xij ≥ 0

(i =1, m; j =1, n). (3)

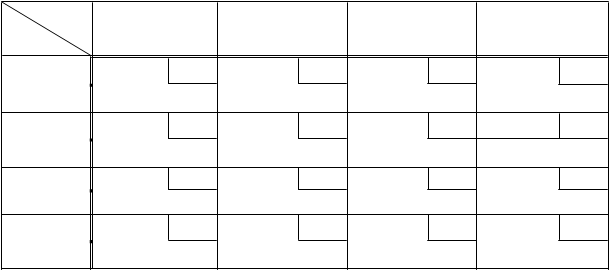
Транспортные задачи удобно записывать табл. 1.

Табл. 1. Транспортная таблица

b j

ai

a 1 x 11

a 2 x 21

b 1

c 11

c 21

x 12

x 22

b 2

c 12

…

c 22

…

…

…

x 1 n

…

x 2 n

bn

c 1 n

c 2 n

… … … …

… … … … …

am xm 1

cm 1

xm 2

cm 2

…

…

xmn

cmn

Рассмотрим открытую транспортную задачу, у которой суммарные запа-

m n

сы поставщиков больше суммарного спроса потребителей:

∑ ai > ∑ bj. Чтобы

i =1

j =1

сделать задачу закрытой вводят фиктивного (n +1) -го потребителя с потребно-

m n

стью

bn +1= ∑ ai − ∑ bj

и стоимостью перевозок 0. В табл. 1 добавляют столбец

i =1

j =1

с этой информацией.

m n

Если же

∑ ai < ∑ bj, то вводится фиктивный (m +1) -й поставщик с запа-

сом

i =1

n m

am +1= ∑ bj − ∑ ai

j =1

и стоимостью перевозок 0. В табл. 1 добавляется строка.

j =1

i =1

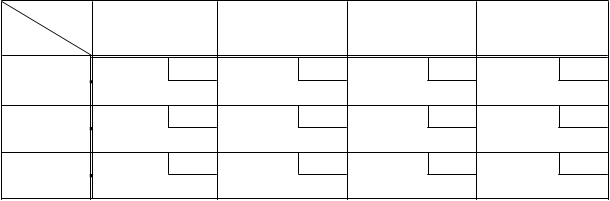
Пример 1. Транспортная задача задана табл. 2.

Табл. 2. Данные задачи

b j 15 15 16 18

ai

4 1 2 1

20

4 6 3 2

5 2 1 4

Т.к.

3 4

∑ ai = 60 < ∑ bj

= 64, то это открытая транспортная задача. Введём

i =1

j =1

фиктивного 4-го поставщика с запасом

a 4 = 64 − 60 = 4

и стоимостью перевозок

0. В табл. 2 добавляем строку и получаем табл. 3.

Табл. 3. Транспортная таблица с фиктивным поставщиком

b j 15 15 16 18

ai

4 1 2 1

4 6 3 2

5 2 1 4

0 0 0 0

2. Закрытая транспортная задача всегда имеет решение. Поэтому важно уметь находить начальный опорный план транспортной задачи, который был бы бли- зок к экстремальному значению целевой функции.

Рассмотрим метод северо-западного угла. Его суть заключается в том, что максимально возможная поставка помещается в северо-западную клетку таблицы. Т.е. максимально возможные поставки заполняют клетки слева напра-

во и построчно.

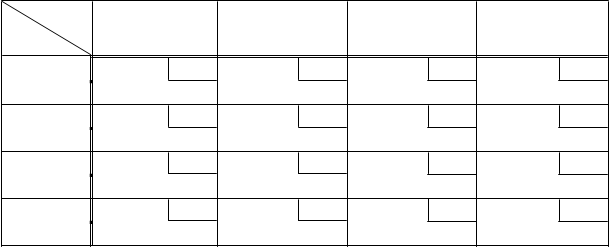
Пример 2. По данным примера 1 составим начальный опорный план с помощью метода северо-западного угла (табл. 4).

Табл. 4. Метод северо-западного угла

b j 15 15 16 18

ai

4 1 2 1

20 15 5

4 6 3 2

30 10 16 4

5 2 1 4

10 10

0 0 0 0

4 4

Начальный опорный план

⎛15 5 0 0 ⎞

⎜ ⎟

X (1) = ⎜ 0 10 16 4 ⎟. Значение целевой

функции:

(1)

1 ⎜ 0 0 0 10 ⎟

⎝ ⎠

⎜ 0 0 0 4 ⎟

Z (X 1

) = 4 ⋅15 +1⋅ 5 + 6 ⋅10 + 3⋅16 + 2 ⋅ 4 + 4 ⋅10 = 60 + 5 + 60 + 48 + 8 + 40 = 221.

Более удачным и, в тоже время, несложным является метод минималь- ной стоимости. Он состоит в том, что максимально возможные поставки необ- ходимо осуществлять для потребителей с наименьшей ценой перевозок слева направо по строке. Остальных – удовлетворять по остаточному принципу, на- ращивая цену.

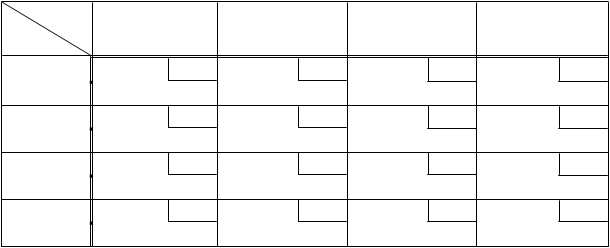
Пример 3. По данным примера 1 составим начальный опорный план с помощью метода минимальной стоимости (табл. 5).

Табл. 5. Метод минимальной стоимости

b j 15 15 16 18

ai

4 1 2 1

20 15 5

4 6 3 2

30 1 16 13

5 2 1 4

10 10

4 4

0 0 0 0

Начальный опорный план

⎛ 0 15 0 5 ⎞

⎜ ⎟

X (2) = ⎜ 1 0 16 13 ⎟. Значение целевой

1 1

функции:

(2)

1 ⎜10 0 0 0 ⎟

⎝ ⎠

⎜ 4 0 0 0 ⎟

Z (X 1

) =1⋅15 +1⋅ 5 + 4 ⋅1+ 3⋅16 + 2 ⋅13 + 5⋅10 =15 + 5 + 4 + 48 + 26 + 50 =148.

Как и ожидалось

Z (X (2)) < Z (X (1)), поэтому в дальнейшем будем ис-

пользовать только метод минимальной стоимости.

Замечание 1. Опорный план транспортной задачи должен содержать

m + n −1 базисных неизвестных, т.е.

m + n −1 заполненных клеток.

Пример 4. Рассмотрим транспортную задачу закрытого типа (табл. 6).

Табл. 6. Транспортная таблица примера 4

b j

ai

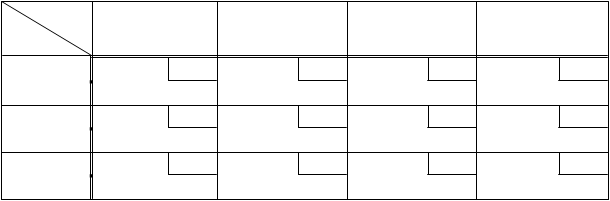600

400 600 800 600

4 3 2 1

2 1 7 9

3 6 8 4

Заполним транспортную таблицу методом минимальной стоимости по-

строчно (табл. 7).

Табл. 7. Заполненная транспортная таблица

b j 400 600 800 600

ai

4 3 2 1

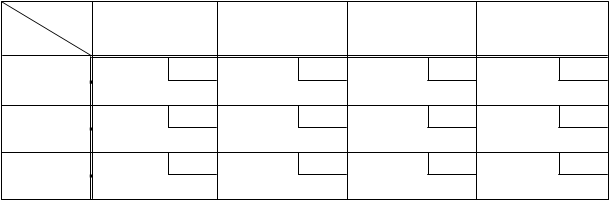600 600

2 1 7 9

800 200 600

3 6 8 4

1000 200 800

В табл. 7 заполнено 5 клеток, а должно быть (замечание 1) заполнено

m + n −1= 3+ 4 −1= 6.

Нужна ещё одна заполненная клетка. Поэтому в одну из пустых клеток

следует поставить 0. Клетка с нулём не должна образовывать цикл с заполнен-

ными клетками.

Нельзя заполнять нулём клетку (2,3), т.к. образуется замкнутый прямо- угольный цикл (2,3); (3,3); (3,1); (2,1); (2,3). Также нельзя заполнять нулём клетку (3,2), т.к. образуется замкнутый прямоугольный цикл (3,2); (3,1); (2,1); (2,2); (3,2). Подробнее о циклах – в следующей лекции.

Другие пустые клетки можно заполнять нулём. Среди допустимых пус-

тых клеток желательно выбирать клетку с наименьшей ценой перевозки. В дан-

ной ситуации – это

возки 0 (табл. 8).

c 13 = 2. Поэтому занесём в пустую клетку (1,3) объём пере-

В этом случае говорят, что получено ацикличное, вырожденное опор-

ное решение.

Т.к. теперь заполненных клеток 6, то замечание 1 учтено.

Табл. 8. Транспортная таблица с учётом замечания 1

b j 400 600 800 600

ai

4 3 2 1

600 0 600

2 1 7 9

800 200 600

3 6 8 4

1000 200 800

Дата добавления: 2014-01-07