Лекция 11. Задачи нелинейного программирования

План

1. Математическая модель задачи нелинейного программирования.

2. Графический метод решения задач нелинейного программирования.

1. При решении сложных задач математического программирования может ока- заться, что линейных функций недостаточно. Рассмотрение реальных экономи- ческих ситуаций требует наиболее полного и точного учёта зависимостей меж- ду факторами, влияющими на целевую функцию и ограничения задачи. Это приводит к построению нелинейных экономико-математических моделей.

Пример 1. Предприятие выпускает два вида продукции

P 1 и

P 2, на кото-

рые расходует три вида ресурсов

S 1, S 2

и S 3 (табл. 1).

С учётом брака расход ресурсов на единицу выпуска продукции состав-

ляет

aij

+ kij ⋅ x j

(i =1, 3;

j =1, 2). Конкуренция и насыщение рынка продукцией

приводит к снижению дохода от реализации одной единицы, т.е.

c j − l j ⋅ x j.

Табл. 1. Данные задачи

Ресурс	Расход ресурса на вы- пуск ед. прод.	Коэфф. увеличения рас- хода ресурса на ед. прод.	Запас ресурса
P 1	P 2	P 1	P 2
S 1	a 11	a 12	k 11	k 12	b 1
S 2	a 21	a 22	k 21	k 22	b 2
S 3	a 31	a 32	k 31	k 32	b 3
Цена реа- лиз. ед. прод. (грн.)	c 1	c 2
Коэфф. снижения цены	l 1	l 2
Количество продукции (ед.)	x 1	x 2

Предприятие стремится выпускать такое количество продукции, чтобы доход от реализации был максимальным. Требуется составить математическую модель задачи.

Решение. Пусть Z – общий доход от реализации (грн.), тогда целевая функция имеет вид:

Z = (c 1 − l 1 ⋅ x 1) x 1 + (c 2 − l 2 ⋅ x 2) x 2 → max. (1)

Запишем ограничения задачи:

⎨(a 21 21 1 1 22 22 2 2 2

⎧(a 11+ k 11 ⋅ x 1) x 1 + (a 12 + k 12 ⋅ x 2) x 2 ≤ b 1

⎩ 31 31 1 1 32 32 2 2 3

⎪ + k ⋅ x) x + (a + k ⋅ x) x ≤ b

⎪(a + k ⋅ x) x + (a + k ⋅ x) x ≤ b

Объёмы производства должны быть неотрицательными:

(2)

x j ≥ 0

(j =1, 2). (3)

Рассмотрение примера окончено.

В общем виде задача нелинеJGйного программирования состоит в отыска-

нии такого вектора неизвестных

X = (x 1; x 2;...; xn), который бы приводил целе-

вую функцию к экстремальному значению:

Z = F (x 1, x 2,..., xn) → max (min). (4)

Система ограничений может содержать как неравенства, так и равенства:

⎪⎧ gi (x 1, x 2,..., xn) ≤ bi

⎨

⎩⎪ gi (x 1, x 2,..., xn) = bi

(i =1, m 1)

(i = m 1 +1, m)

(5)

Среди искомых переменных могут быть отрицательные:

x j ≥ 0

(j =1, n 1); x j < 0

(j = n 1 +1, n). (6)

Задачу (4)-(6) называют математической моделью задачи нелинейного

программирования (НЛП), если хотя бы одна из функций F или gi

(i =1, m)

является нелинейной. Для решения задач НЛП общего метода нет и они реша-

ются сложнее, чем задачи линейной оптимизации.

2. Если задача НЛП имеет две искомые переменные, то её можно решить гра-

фическим методом.

Пример 2. Предприятие выпускает два вида продукции

P 1 и

P 2, на кото-

рые расходует три вида ресурсов

S 1, S 2

и S 3 (табл. 2).

Табл. 2. Данные задачи

Ресурс	Расход ресурса на выпуск единицы продукции aij (i =1, 3; j =1, 2)	Запас ре- сурса bi
P 1	P 2
S 1
S 2
S 3
Цена реализ. ед. прод. c j (тыс. грн.)
Коэфф. снижения це- ны l j
Количество продук- ции x j (ед.)	x	x

1 2

Кризисные явления, конкуренция и насыщение рынка данной продукцией приводит к снижению дохода от реализации одной единицы по формуле

c j − l j ⋅ x j. Требуется найти такой план выпуска продукции, который бы макси-

мизировал общий доход от её реализации.

Решение. Пусть Z – общий доход от реализации (тыс. грн.). Составим математическую модель задачи НЛП.

Z = (100 − x 1) x 1 + (140 − x 2) x 2 → max, (7)

⎧4 x 1+ 6 x 2 ≤ 450

⎪

⎩ 1 2

⎨2 x 1+ 2 x 2 ≤160

⎪3 x + 2 x ≤ 210

(8)

x j ≥ 0

(j =1, 2). (9)

ОДР (8)-(9) – это многоугольник OABCD (рис. 1) с вершинами

O (0; 0),

A (0; 75),

B (15; 65), C (50;30) и

D (70; 0).

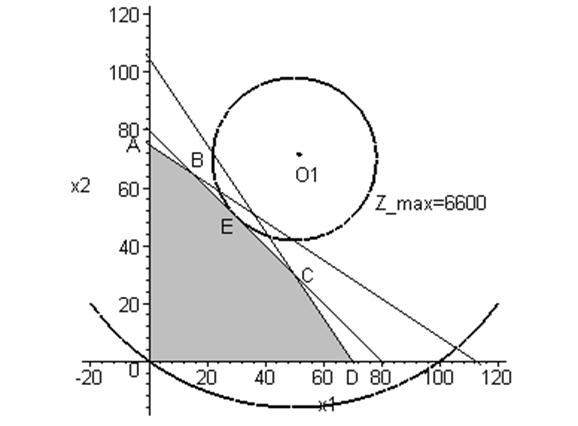
Рис. 1. Иллюстрация графического метода решения

Преобразуем целевую функцию (7):

2 2

Z =100 x 1 − x 1

+140 x 2 − x 2;

2 2

− Z = (x 1

−100 x 1 + 2500) − 2500 + (x 2

−140 x 2 + 4900) − 4900;

7400 − Z = (x 1 − 50)

2 + (x − 70)2;

()2 2 2

7400 − Z

= (x 1 − 50)

+ (x 2 − 70).

Получено уравнение окружности с центром

O 1(50; 70)

и переменным ра-

диусом R =

7400 − Z. Т.к.

R ≥ 0, то границы изменения целевой функции:

0 ≤ Z ≤ 7400. Чем меньше радиус окружности, тем больше значение целевой

функции.

Рассмотрим окружность с нулевым радиусом

02 = (x

− 50)2 + (x

− 70)2,

т.е. точку

1 2

O 1(50; 70). Эта точка лежит вне ОДР и не может быть решением. По-

немногу увеличивая радиус, будем приближать окружность к ОДР. Точка пер-

вого касания окружности и ОДР будет оптимальным планом, максимизирую-

щим целевую функцию. Назовём эту точку

E (x 1; x 2). Видно, что она принадле-

жит прямой

2 x 1 + 2 x 2 =160

(x 1 + x 2 = 80) или

x 2 = − x 1 + 80.

Точка

E (x 1; x 2)

будет также принадлежать окружности

7400 − Z = (x 1 − 50)

2 + (x − 70)2

. Выразим вертикальную координату

2 2

x 2:

(x 2 − 70)

= 7400 − Z − (x 1 − 50);

2

x 2 − 70 = ±

7400 − Z − (x 1 − 50).

Т.к. точка

E (x 1; x 2)

принадлежит нижней части окружности, то перед кор-

нем следует оставить только знак «минус»:

x 2 =−

7400 − Z − (x 1 − 50)

+ 70.

Получены две функции – прямая

x 2 = − x 1 + 80

и полуокружность

x 2 =−

7400 − Z − (x 1 − 50)

+ 70, графики которых имеют общую точку

E (x 1; x 2). Это точка касания. Поэтому угловые коэффициенты касательных

k 1 и

k 2 совпадают. Вычислим их, воспользовавшись геометрическим смыслом про-

изводной:

k = (− x + 80)/ = −1;

1 1 x

1

k 2 = (−

7400 − Z − (x 1 − 50)

/

)

+ 70

x 1

= −2(x 1 − 50)

−2 7400 − Z − (x 1 − 50)

Составим систему трёх уравнений с тремя неизвестными решим её:

⎧

x 1,

x 2 и Z, и

⎪ x 2 = − x 1 + 80

⎧ x 2 = − x 1 + 80

⎪

⎪

⎪ x =−

7400 − Z − (x

− 50)2 + 70

x = −

7400 − Z − (x

− 50)2 + 70

⎨ 2 1

⎩

⎪

⎨ 2 1

⎪

⎪ (x 1 − 50)

= −1

⎪− 7400 − Z − (x

− 50)2 = x

− 50

⎪ 7400 − Z − (x 1

⎩ 1 1

− 50)2

2 1

⎧ x = − x + 80

⎪

⎨ x 2 = x 1 − 50 + 70

⎪

⎧ x + 20 = − x + 80

⎪

1 1

⎨ x 2 = x 1 + 20

⎪

− 7400 − Z − (x

− 50)2 = x

− 50

− 7400 − Z − (x

− 50)2 = x

− 50

1 1

⎧ x = 30

⎪

⎨ x 2 = x 1 + 20

⎪

1 1

⎧ x 1 = 30

⎪

⎨ x 2 = 50

⎪

− 7400 − Z − (x

− 50)2 = x

− 50

⎩ Z = 6600

Откуда получим

⎪⎩ 1 1

E (30;50).

Ответ: Оптимальный план выпуска продукции

x * = 30

(ед.) и

x * = 50

(ед.), при котором

Z max

= 6600 (тыс. грн.).

Решённая задача позволяет выработать общий подход в том случае, когда оптимальное решение находится на границе ОДР, но не в угловой точке.

Пусть график целевой функции

x 2 =

f (x 1, Z)

касается графика ограниче-

ния

x 2 = g (x 1). Следовательно, они имеют общую точку, координаты которой

можно найти, решив систему уравнений:

⎧

⎪ x 2 =

⎪

f (x 1, Z)

⎨ x 2 = g (x 1)

⎪[ f (x, Z)]/

= [ g (x)]/

⎪ 1 x 1 x

⎩ 1 1

Замечание 1. Если бы задача НЛП (7)-(9) была задачей на минимум, т.е.

Z → min, то её оптимальным планом оказалась бы угловая точка ОДР

O (0; 0).

Этот факт отражён на рис. 1 (окружность большего радиуса достигает начала координат).

Наиболее распространёнными среди задач НЛП экономической направ-

ленности являются задачи квадратичного программирования. В таких зада- чах целевая функция является кривой второго порядка: окружностью, эллип- сом, гиперболой или параболой. Левые части ограничений – линейные функ- ции. При необходимости налагается условие не отрицательности. Пример 2 – типичная задача квадратичного программирования.

Домашнее задание. Повторить из курса высшей математики кривые вто-

рого порядка.

Дата добавления: 2014-01-07