Лекция 12. Метод множителей Лагранжа

План

1. Метод множителей Лагранжа для задач нелинейного программирования двух переменных.

2. Практическая реализация метода множителей Лагранжа.

1. Рассмотрим задачу НЛП двух переменных

x 1 и

x 2, все ограничения которой

являются равенствами и на знак неизвестных не налагается никаких условий,

т.е.

Z = F (x 1, x 2) → max (min); (1)

⎪

⎧ g 1 (x 1, x 2) = b 1,

⎪ g 2 (x 1, x 2) = b 2,

⎨

⎪......................

⎪⎩ gm (x 1, x 2) = bm.

(2)

Модель (1)-(2) называют математической моделью классической зада- чи нелинейной оптимизации. Такие задачи решаются методом множителей Лагранжа. Алгоритм метода следующий.

1) Составить функцию Лагранжа

L (x 1, x 2,λ1,λ2,...,λ m) = F (x 1, x 2) + λ1[ b 1 − g 1 (x 1, x 2)]+ λ2[ b 2 − g 2 (x 1, x 2)]+...+

+λ m [ bm − gm (x 1, x 2)], (3)

где

λ1,λ2,...,λ m

– множители Лагранжа.

Смысл множителей Лагранжа такой же, как и двойственных оценок в

задачах линейного программирования. Т.е. λ i

(i =1, m) показывают, на сколько

единиц изменится значение целевой функции в оптимальном решении, если

правая часть i -го ограничения bi

увеличится на одну единицу.

2) Найти частные производные первого порядка функции Лагранжа (3) по

всем неизвестным:

∂ L, ∂ L, ∂ L, ∂ L

,..., ∂ L.

∂ x 1

∂ x 2

∂λ1

∂λ2

∂λ m

3) Согласно необходимому условию экстремума, приравнять частные производные к нулю:

⎧ ∂ L

⎪∂ x

⎪

⎪ ∂ L

⎪∂ x

⎪ 2

∂λ

⎪ ∂ L

⎪

⎨ 1

⎪ ∂ L

⎪

⎪∂λ2

= 0,

= 0,

= 0,

= 0,

⎪............

⎪

∂λ

⎪ ∂ L

⎪

⎩ m

= 0.

Решить полученную систему уравнений и определить стационарные точки

функции Лагранжа:

Q (x (1), x (1), λ (1), λ (1),..., λ

(1)),

(2) (2) (2) (2) (2)

1 1 2 1 2 m

(k) (k) (k) (k) (k)

Q 2 (x 1

, x 2

, λ1

, λ2

,..., λ m

),…, Qk (x 1

, x 2

, λ1

, λ2

,..., λ m).

4) Для применения достаточных условий экстремума, следует найти ча-

стные производные второго порядка функции Лагранжа по переменным

x 1 и

x 2:

∂ 2 L

A =,

∂ x 2

∂ 2 L

B =,

∂ x 1∂ x 2

∂ 2 L A B

C =. Составить определитель ∆=

∂ x 2 B C

и вычис-

лить его значение в стационарных точках Q 1, Q 2,…, Qk.

(j) (j) (j) (j) (j)

Если

∆(Q j) > 0

(j =1, k), то точка

Q j (x 1

, x 2

, λ1

, λ2

,..., λ m

) является

точкой экстремума, причём при

A (Q j) > 0

будет минимум, а при

A (Q j) < 0 –

1 2

максимум. Ответ должен содержать оптимальный план

X * = (x (j); x (j))

и экс-

тремальное значение целевой функции исходной задачи (1)-(2), т.е.

Z min(max) = Z (X *).

Если

∆(Q j) < 0

(j =1, k), то экстремума в точке Q j

нет. Такая ситуация

может иметь место для всех точек Q j

(j =1, k). Тогда в ответе следует указать,

что задача нелинейного программирования решений не имеет.

Если же

∆(Q j) = 0

(j =1, k), то экстремум в точке Q j

может существо-

вать, а может и не существовать. Такая ситуация может иметь место для всех

точек Q j

(j =1, k). Тогда в ответе следует указать, что вопрос о наличии опти-

мального плана остаётся открытым и задача требует дополнительных исследо-

ваний. Такие исследования трудоёмки и выходят за рамки учебной программы.

2. Продемонстрируем метод множителей Лагранжа на конкретном примере.

Пример 1. Решить задачу НЛП:

2 2

Z = x 1

+ x 2

+ 6 x 2 − 5 → min,

⎩ x 1 2

⎧ x 1 ⋅ x 2 = 3,

⎨ + x = 4.

Решение. Это классическая задача нелинейной оптимизации, поэтому

применим метод множителей Лагранжа.

1) Составим функцию Лагранжа:

2 2

L (x 1, x 2, λ1, λ2) = x 1

+ x 2

+ 6 x 2 − 5 + λ1[3 − x 1 ⋅ x 2] + λ2[4 − x 1 − x 2].

2) Найдём частные производные:

∂ L ∂ L ∂ L ∂ L

∂ x 1

= 2 x 1 − λ1 ⋅ x 2 − λ2,

∂ x 2

= 2 x 2 + 6 − λ1 ⋅ x 1 − λ2,

∂λ1

= 3 − x 1 ⋅ x 2,

∂λ2

= 4 − x 1 − x 2.

3) Проверяем необходимое условие экстремума:

⎪

⎧2 x 1− λ1 ⋅ x 2 − λ2 = 0,

⎪2 x 2+ 6 − λ1 ⋅ x 1 − λ2 = 0,

⎧2 x 1− λ1 ⋅ x 2 − λ2 = 0,

⎪2 x 2− λ1 ⋅ x 1 − λ2 = −6,

⎨ ⎨ (1) (1)

⎪

⎪3 − x 1 ⋅ x 2 = 0,

⎪1) x 1

= 3, x 2

=1,

4 − x 1 − x 2 = 0.

⎪2) x (2) =1, x (2) = 3,

⎩ 1 2

⎧1) x (1) = 3, x (1) =1, λ (1) =1, λ (1) = 5,

⎪ 1 2 1 2

⎨

⎪2) x (2) =1, x (2) = 3, λ (2) = −5, λ (2) =17.

⎩ 1 2 1 2

Получены стационарные точки Q 1 (3;1;1;5)

и Q 2 (1;3; −5;17).

4) Проверяем выполнение достаточных условий экстремума. Найдём

∂2 L

A =

∂ x 2

= 2,

∂2 L

B =

∂ x 1∂ x 2

= −λ1 и

∂2 L

C =

∂ x 2

= 2. Получим определитель

A B

∆= =

B C

−λ1

−λ1

2

= 4 − λ 2.

Т.к.

∆(Q 1) = 3 > 0 и

A (Q 1) = 2 > 0, то точка

Q 1(3;1;1;5)

является точкой ми-

нимума функции Лагранжа. Значит,

X * = (3;1)

и Z min =11.

Т.к.

∆(Q 2) = −21 < 0, то точка

Q 2(1;3; −5;17)

не является точкой экстрему-

ма функции Лагранжа.

Ответ:

X * = (3;1),

Z min =11.

Пример 2. Решить задачу НЛП:

4 4 2 2

Z = x 1

+ x 2

− 2 x 1

+ 4 x 1 x 2 − 2 x 2

→ min,

x 1 + x 2 = 0.

Решение. Это классическая задача нелинейной оптимизации, поэтому

применим метод множителей Лагранжа.

1) Составим функцию Лагранжа:

1 2

4 4 2 2

L (x 1, x 2, λ1) = x 1

+ x 2

− 2 x 1

+ 4 x 1 x 2 − 2 x 2

+ λ1[− x 1 − x 2 ].

2) Найдём частные производные:

∂ L = 4 x 3 − 4 x

+ 4 x

− λ,

∂ L = 4 x 3 + 4 x

− 4 x

− λ,

∂ L = − x

− x.

∂ x 1

1 1 2 1

∂ x 2

2 1 2 1

∂λ1

3) Проверяем необходимое условие экстремума:

⎧4 x 3 − 4 x

+ 4 x

− λ = 0,

⎧−4 x 3 + 4 x

+ 4 x

− λ = 0,

⎧−8 x 3 +16 x

= 0,

1 1 2 1

⎪

2 2 2 1 2 2

⎪ ⎪

4 x 3 + 4 x

− 4 x

− λ = 0,

4 x 3 − 4 x

− 4 x

− λ = 0,

4 x 3 − 8 x

− λ = 0,

⎨ 2 1 2 1

⎨ 2 2 2 1

⎨ 2 2 1

⎪− x − x = 0.

⎪⎩ 1 2

⎪ x = − x.

⎪⎩1 2

⎪ x = − x.

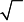
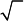⎪⎩1 2

⎧−8 x

(x 2 − 2) = 0,

⎧ x (1) = 0, x (2) = −

2, x (3) = 2,

2 2

⎪4 x 3 − 8 x

− λ = 0,

2 2 2

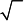⎪λ(1) = 0, λ (2) = 0, λ (3) = 0,.

⎨ 2 2 1

⎨ 1 1 1

1 2

⎪ x = − x.

⎪ x (1) = 0, x (2) =

2, x (3) = − 2.

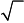
1 1 1

1 2 1 2

Получены стационарные точки Q 1 (0; 0;0), Q 2 (2; −

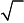
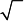2; 0)

и Q 3 (−

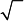
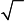2; 2; 0).

4) Проверяем выполнение достаточных условий экстремума. Найдём

A = ∂

L =12 x 2 − 4, B =

∂2 L

= 4 и C =

∂2 L

=12 x 2 − 4. Получим определитель

∂ x 2 1

∂ x 1∂ x 2

∂ x 2 2

A B

∆= =

B C

12 x 2 − 4 4

4 12 x 2 − 4

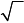
=144 x 2 x 2 − 48 x 2 − 48 x 2.

Т.к.

∆(Q 1) = 0, то вопрос о наличии экстремума в точке

Q 1 (0; 0;0)

остаётся

открытым и нужны дополнительные исследования.

Т.к.

∆(Q 2) = 384 и

A (Q 2) = 20 > 0, то точка

Q 2(2; −

2; 0)

является точ-

кой минимума функции Лагранжа. Значит,

X 1* = (2; −

2) и

Z min = −8.

Т.к.

∆(Q 3) = 384 и

A (Q 3) = 20 > 0, то точка

Q 3 (−

2; 2; 0)

является точкой

минимума функции Лагранжа. Значит,

X 2* = (−

2; 2) и

Z min = −8.

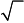
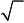Ответ:

X 1* = (2; −

2),

X 2* = (−

2; 2),

Z min = −8.

ЗАКЛЮЧЕНИЕ

Данный курс содержит основы математического программирования в сжатом виде. Отдельные классы задач в лекциях не рассматривались. Дадим о них краткую информацию.

Задачи параметрического программирования содержат некоторые па-

раметры, от которых зависит целевая функция и ОДР. Если целевая функция представляет собой отношение (дробь) двух линейных функций, то имеет место

задача дробно-линейного программирования. Задача математического про- граммирования, содержащая случайные величины, называется задачей стохас- тического программирования. Если процесс решения задачи математическо-

го программирования является многоэтапным и оптимальные решения нахо- дятся для разных моментов времени, то речь идёт о задаче динамического программирования.

Студентам предлагается самостоятельно изучить эти типы задач (напри- мер, по учебному пособию [1]). При необходимости следует проконсультиро- ваться у преподавателя.

Приложения содержат лекционный материал для самостоятельного озна- комления. В этих лекциях рассматриваются некоторые практические задачи, сводящиеся к задачам математического программирования.

Автор будет признателен своим коллегам, студентам и всем интересую- щимся лицам за дельные рекомендации, которые могли бы способствовать улучшению качества лекций.

Приложение А. ИНВЕСТИЦИОННЫЕ ЗАДАЧИ И НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Дата добавления: 2014-01-07