Персией

Di, выборочным средним квадратическим (стандартным) откло-

нением σ i:

m = 1

i T

T

T

∑

t =1

Ri (t),

D = 1 (R (t) − m)2,

T − 1

i ∑ i i

t =1

σ i =

Di.

число

Заметим, что в формуле для выборочной дисперсии в знаменателе стоит

T −1. Эта поправка внесена с целью получения несмещённой оценки

дисперсии. Поправкой обычно пренебрегают, если объем выборки T достаточ-

но большой. Это означает, что при

T < 20

в формулу подставляют

T −1, а при

T ≥ 20

– подставляют T.

Если дисперсия эффективности равна нулю, то эффективность не откло- няется от математического ожидания, т.е. нет неопределённости и риска. Чем больше дисперсия, тем в среднем больше отклонение, т.е. выше неопределён-

ность и риск. Поэтому величину дисперсии считают мерой риска, а σ i

называ-

ют риском i -го актива. Инвестор заинтересован в увеличении ожидаемой эф-

фективности

mi. С другой стороны, важно уменьшить риск.

Кроме индивидуальных числовых характеристик

mi,

Di,

σ i, рассчиты-

вают характеристики взаимовлияния активов – выборочные ковариации эффективностей:

1 T

V = (R (t) − m)(R

(t) − m).

T − 1

ij ∑

t =1

i i j i

Заметим, что Vij

= V ji

и Vii = Di = σ i.

2. Считается, что характеристик mi

и σ i

достаточно для отбора «перспектив-

ных» ценных бумаг в портфель. Акции с отрицательным показателем mi не

должны включаться в портфель. Оставшиеся ценные бумаги подлежат рас-

смотрению.

По сути дела, сравниваются пары чисел (mi;σ i). Если какой-то актив за-

ведомо «проигрывает» другому, то он исключается из портфеля. Такой способ

отбора называют методом последовательных сравнений.

Например, если имеется возможность выбора между двумя акциями, при-

чем

mi > m j, а

σ i = σ j, то инвестор предпочтёт i -ю ценную бумагу. Если же

mi = m j, а σ i > σ j, то инвестор выберет j -ю акцию. В ситуации

инвестор предпочтет i -ю ценную бумагу.

mi > m j, σ i < σ j

Однако, если

mi > m j,

σ i > σ j

(или

mi < m j,

σ i < σ j), то однозначного ре-

шения нет и выбор инвестора будет зависеть от его склонности к риску. Реко- мендуется включать в портфель обе акции и уже внутри портфеля решать во- прос о том, какую часть капитала вкладывать в конкретную ценную бумагу.

Пример 1. В табл. 1 приведены цены акций

Si (t) (грн.) пяти корпораций

за 10 биржевых дней. Здесь i – номер акции (i =1, 5), t – номер биржевого дня

(t =1,10).

Табл. 1. Цены акций пяти корпораций

t
S 1(t)
S 2(t)
S 3(t)
S 4(t)
S 5(t)

Требуется: 1) провести статистический анализ эффективностей акций; 2)

отобрать «перспективные» ценные бумаги в фондовый портфель.

Решение. 1) Наличие 10-ти данных по стоимостям акций определяет T = 9

временных периодов, на каждом из которых рассчитывается эффективность

Ri (t),

i =1, 5,

t =1, 9. От выборок с 10-ю ценами акций (грн.) осуществляется

переход к выборкам с 9-ю эффективностями (%) (табл. 2):

Табл. 2. Эффективности акций пяти корпораций

t
R 1(t)				66,67				6,67	12,5
R 2(t)				233,33	-50			6,67
R 3(t)		33,33						13,33
R 4(t)					-50				5,56
R 5(t)	-11,11	-6,25		-33,33	-90				66,67

Например,

R (9) = S 1 (10) − S 1 (9) ⋅100% = 18 −16 ⋅100% =12, 5%.

S 1 (9) 16

По всем выборкам рассчитаем выборочные средние mi

и средние квадра-

тические отклонения σ i

эффективностей. В Microsoft Excel – с помощью функ-

ций СРЗНАЧ() и СТАНДОТКЛОН(), соответственно. Функции вызываются опцией «fx» – «Вставка функции». Формируем табл. 3.

Таблица 3. Индивидуальные числовые характеристики акций

i	mi (%)	σ i (%)
	48,4259	67,1188
	65,5556	110,8553
	30,1852	33,0030
	47,2840	83,1482
	13,9969	80,6651

2) Определим «перспективные» ценные бумаги (рис. 1).

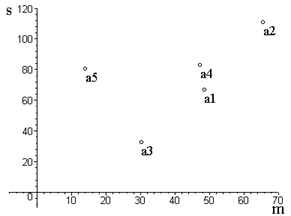
Рис. 1. Точечная диаграмма отбора акций в портфель

Методом последовательных сравнений убеждаемся в том, что «перспек- тивными» акциями являются а3, а1, а2. Из них и следует формировать портфель ценных бумаг.

Можно использовать и другой способ отбора. На точечной диаграмме строится нижняя огибающая ломаная, все звенья которой имеют положитель- ный коэффициент наклона (рис. 2).

Рис. 2. Графический способ отбора акций в портфель

Точки, попавшие на эту ломаную, определяют «перспективные» акции. Судя по рис. 2, в портфеле ценных бумаг должны остаться акции а3, а1, а2. Та- кой способ отбора называют методом нижней огибающей ломаной.

Дата добавления: 2014-01-07