Метод узловых потенциалов

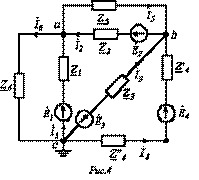Идея метода основана на первом законе Кирхгофа. За неизвестные принимаются потенциалы узлов, по которым с помощью закона Ома для участка цепи с источником ЭДС затем находятся токи в ветвях. Потенциал одного из узлов (любого) принимается равным нулю. Число неизвестных потенциалов, а следовательно, и число уравнений равно 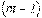, т.е. числу ветвей дерева .

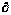Для схемы на рис. 4 принимается .

Полагая, что 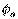и 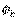известны, значения токов на основании закона Ома для участка цепи с источником ЭДС можно представить в виде:

Уравнение по первому закону Кирхгофа для узла а:

Подстановка в него значения токов

и последующая группировка дает

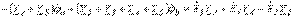Аналогичная запись для узла b:

Для составления системы уравнений также может быть использован формальный способ

1. В левой части i- го уравнения со знаком “+” записывается потенциал 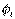i- го узла, для которого составляется данное i- е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i- му узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i- му и k- му узлам.

Все компоненты 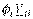, стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем 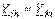. Это равенство как и в методе контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2. В правой части i- го уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих к i- му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i- му узлу, в противном случае ставится знак “-”. Если в подходящих к i- му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

Дата добавления: 2014-01-07