Амплитудно-частотная характеристика

усилителя

Зависимость коэффициента усиления от частоты называется частотной или амплитудно-частотной характеристикой усилителя.(рис. 3.10). Диапазоном рабочих частот называют полосу частот от низшей рабочей частоты f_Н до верхней рабочей частоты f_В. Для оценки величины частотных искажений (изменений К от частоты) используют коэффициент частотных искажений М равный отношению модуля коэффициента усиления на средней частоте К_СР к модулю коэффициента усиления на рассматриваемой частоте:

M=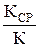. (3.6.1)

Коэффициент частотных искажений часто выражают в логарифмических единицах; для перевода их из относительных единиц в децибелы и обратно используют соотношения:

М_[дб]=20lgМ, (3.6.2)

M=10^0.05M[дб]. (3.6.3)

Общий коэффициент частотных искажений вносимый n-каскадами равен:

М=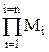, (3.6.4)

где М_i- коэффициент частотных искажений вносимый i-м каскадом или элементом.

Допустимый коэфициент частотных искажений на нижней частоте М_доп.н. равен произведению допустимых коэфицентов частотных искажений вносимых разделительными конденсаторами М_{доп.с.р.} и конденсатором С_Э - М_{доп.с.э.}

М_доп.н=М_доп.с.р×М_доп.с.э, (3.6.5)

М_Н=М_СР×М_СЭ , (3.6.6)

М_СР=М_С1×М_С2. (3.6.7)

Из условия М_СР£М_доп.с.р определяются величины емкости конденсаторов С₁ и С₂, вносящих частотные искажения на нижней частоте f_Н, где М_ДОП.Н.Р- допустимый коэффициент частотных искажений на низкой частоте разделительными конденсаторами, М_доп.с.э.

М_доп.с.р=М_С1×М_С2 , (3.6.8)

откуда М_С1=М_С2=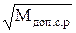. (3.6.9)

Для определения емкости конденсаторов С₁ и С₂ используют неравенства:

С₁³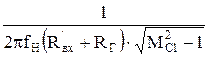, (3.6.10)

С₂³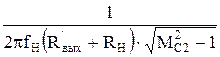. (3.6.11)

При шунтировании R_Эс конденсатором R_Эс=r_Э.

Емкость конденсатора С_Э определяют по формуле:

С_Э³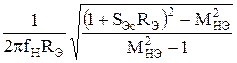, (3.6.12)

где М_НЭ- допустимый коэффициент частотных искажений для конденсатора С_Э ,

S_Эс=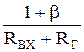- крутизна тока цепи эмиттера в схеме.

Частотные искажения на высокой частоте могут вноситься транзистором из-за зависимости b от частоты и вследствие зависимости входного комплексного сопротивления следующего каскада от частоты (или комплексного сопротивления нагрузки от частоты).

М_В=М_Т*М_НГ<М_В.ДОП, (3.6.13)

где М_Т- коэффициент частотных искажений вносимых транзистором; М_НГ- коэффициент частотных искажений вносимых нагрузкой.

Если сопротивление нагрузки на верхней частоте можно считать активным, то М_НГ=1.

М_Т=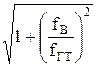, (3.6.14)

где f_ГТ- граничная частота усиления транзистора.

f_ГТ³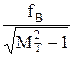. (3.6.15)

Если f>10⁵ и нагрузкой является такой же каскад, то необходимо расчитывать М_НГ, которое равно:

M_HГ=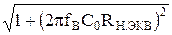, (3.6.16)

где С₀- эквивалентная последовательная емкость нагрузки,

R_Н.ЭКВ- эквивалентное последовательное сопротивление нагрузки.

Для такого же следующего каскада:

R_H.ЭКВ=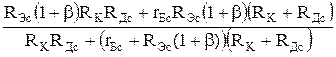, (3.6.17) R_H.ЭКВ»R_Д||R_K||R_Э(1+b), (3.6.18)

где R_Д=R_1с||R_2с, индекс "с" относится к параметрам следующего каскада.

С₀»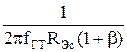+С_КсК_с»С_Эбс, (3.6.19)

где К_с- коэффициент усиления следующего каскада, С_Кс- коллекторная емкость следующего каскада.

Дата добавления: 2014-01-07