Принципы построения системы единиц величин

Лекция 3. Единицы величин и размерности.

Сравнение измерительных шкал

Шкалы	Операции, определённые на шкалах	Наличие нуля	Характеристики шкал
Порядка	Логические	–	Нельзя определить не только, чему равно значение q 1измеряемой величины, но и на сколько оно больше или меньше значения q 2
Интервалов	Математические: аддитивные (+, –)	Услов-ный	Нельзя определить значение измеряемой величины. В результаты измерений могут вноситься аддитивные поправки, но использование поправочных множителей невозможно.
Отношений	Математические: аддитивные и мультиплика-тивные (+, –, ×,:)	Естест-венный	Можно определить значение измеряемой величины. В результаты измерений могут вноситься как аддитивные, так и мультипликативные поправки.

Системы физических величин, существовавшие
в разные времена и в разных государствах, имели
много отличий:

они использовали разные меры,

они имели разные кратности используемых единиц,

они имели разное количество основных и производных единиц.

Система физических величин – Совокупность физических величин, образованная в соответствии
с принятыми принципами, когда одни величины принимают за независимые (основные величины),
а другие (производные величины) определяют
как функции независимых величин.

При всех этих различиях, существовавшие системы физических величин имели общие черты:

наличие общепризнанных (узаконенных
для данного государства) мер для воспроизведения единиц физических величин,

наличие связей между отдельными мерами
для образования производных единиц,

наличие системы передачи размеров единиц физических величин.

Передача размера единицы – приведение размера единицы физической величины, хранимой средством измерений, к размеру единицы, воспроизводимой или хранимой эталоном

Взаимосвязи физических величин в системе отражаются
с помощью такого важного понятия как размерность – (от dimension). Размерность величины представляет собой выражение в форме степенного многочлена,
раскрывающее связь физической величины Q
с основными физическими величинами.

Например, в системе LMT, принятой в механике,
в которой в качестве основных единиц используются
длина L, масса M, время T, размерность имеет вид:

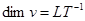Показатели a, b, g называются показателями размерности.

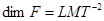В частности, размерность скорости,
а размерность силы

Над размерностями можно производить действия: умножения, деления, возведения в степень и извлечение корня.

Понятие размерности широко используется:

для перевода единиц из одной системы в другую;

для проверки правильности расчётных формул, полученных в результате теоретического вывода;

при выяснении зависимости между ними;

в теории физического подобия.

Размерность производной величины – простейшее уравнение связи, определяющее величину,
с коэффициентом пропорциональности равным единице.

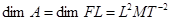Однако при этом размерность не отражает физическую природу величины. В частности, у ряда различных
по природе величин размерности оказываются одинаковыми.

Например, работа и момент силы имеют одну и ту же размерность:

Кроме того, размерность не раскрывает способ измерения величины, за исключением простейших случаев, когда уравнение связи совпадает с выражением размерности,
что к примеру характерно для площади квадрата.

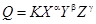1. Уравнения связи между величинами, в которых под буквенными символами понимаются физические величины:

Коэффициент К не зависит от выбора единиц величин.

Пример – площадь треугольника S равна половине произведения основания L на высоту h: S =0,5 Lh, т.е. К =0,5

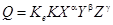2. Уравнения связи между числовыми значениями величин,
в которых под буквенными символами понимаются числовые значения физических величин:

Коэффициент К_e зависит от выбора системы единиц.

Пример – уравнение связи между площадью треугольника
в квадратных миллиметрах, при условии, что основание и высота измеряются в метрах. При этом К_e =10^-6 мм²/м²

Зависимости между единицами измерений,
проявляющиеся в физических законах, позволяют получать производные единицы системы, понятие которых впервые было введено К.Гауссом.

Наименования и обозначения производных величин могут быть получены:

из наименований и обозначений основных единиц;

с использованием специальных наименований и обозначений;

из наименований и обозначений основных и специальных наименований и обозначений производных единиц;

с использованием кратных и дольных приставок и множителей.

Производные единицы бывают: когерентными и некогерентными.

Когерентной называется производная единица, связанная
с другими единицами системы уравнением, в котором числовой множитель принят равным единице.

Например, единицу скорости образуют с помощью уравнения, определяющего скорость прямолинейного равномерного движения точки: v = L / t,

где L – длина пройденного пути; t – время движения.

Подстановка вместо L и t их единиц дает v = 1 м/с.

Следовательно, единица скорости является когерентной

Если уравнение связи содержит числовой коэффициент, отличный от единицы, то для образования когерентной единицы SI в правую часть уравнения подставляют величины со значениями в единицах SI, дающие после умножения на коэффициент общее числовое значение, равное единице.

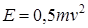Например, если для образования когерентной единицы энергии применяют уравнение

где m – масса тела; v – его скорость, то когерентную единицу энергии можно образовать двумя путями:

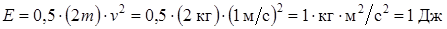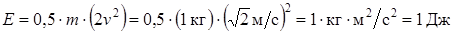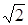Следовательно, когерентной единицей SI является джоуль, равный ньютону, умноженному на метр. В рассмотренных случаях он равен кинетической энергии тела массой 2 кг, движущегося со скоростью 1 м/с, или тела массой 1 кг, движущегося со скоростью м/с.

Международная система единиц (SI)

Исторически сложилось так, что закономерные научно обоснованные связи были установлены сначала в области геометрии и кинематики, затем динамики, термодинамики и электромагнетизма.

Последовательно строились и системы единиц.

В связи с этим общего решения всей совокупности уравнений связи можно было избежать, а их решение свести к последовательному определению единиц
в соответствующих разделах физики.

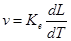В геометрии и кинематике для установления связей между единицами достаточно уравнения

где v – скорость, L – длина, T – время.

Первоначально (до 1983 г.) в качестве основных величин были выбраны единицы измерения длины и времени,
а в качестве производной – скорость.

В 1983 г. основными были названы единицы измерения времени и скорости, при этом скорости света в вакууме было придано точное, в принципе произвольное значение
с = 299 792 458 м/с. Длина и ее единица – метр, по существу, стали производными. Однако формально длина в SI остается основной величиной, и ее единица определяется следующим образом: метр – расстояние, которое проходит свет в вакууме за 1/299 792 458 долю секунды.

Для образования системы единиц в области геометрии
и кинематики следует добавить уравнения связи
для площади (например, квадрата), объема (например, куба), ускорения и т.д.

При добавлении уравнений каждый раз вводится одна новая величина и соответственно одно уравнение связи, при этом разность между количеством основных и производных единиц, равная 2, сохраняется, и система единиц оптимальна.

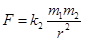
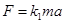При переходе к динамике рассмотренное уравнение дополняется уравнениями второго закона Ньютона

и закона всемирного тяготения

Были добавлены два уравнения связи и введены две новые величины – масса и сила, разность между количеством основных и производных величин не изменилась.

При добавлении остальных уравнений механики
для давления, работы, мощности и т.д.
рассматриваемая разность также не изменяется.

Принимая k ₁ = k ₂ = 1, сила и масса стали бы производными физическими величинами. Считая, что m = m ₁ = m ₂, из уравнений получаем m = ar ², т. е. единица массы есть масса такой материальной точки, которая сообщает единичное ускорение любой другой материальной точке, находящейся на единичном расстоянии. Такая производная единица массы имеет размерность м³/с и примерно равна 1,5×10¹⁰ кг.

Следует отметить, что точность воспроизведения единицы массы при таком ее определении была бы весьма низкой. Поэтому ввели "лишнюю" основную единицу – килограмм (единицу массы). При этом во втором законе Ньютона требовалось сохранить коэффициент пропорциональности. Он был оставлен в законе всемирного тяготения.
Мировая константа – гравитационная постоянная
g = (6,6720 ± 0,041)×10¹¹ (Нм²)/кг².

Килограмм — масса международного прототипа килограмма, представляющего собой цилиндр из сплава платины и иридия.

Эталон килограмма является единственным уничтожимым эталоном из всех эталонов основных единиц SI.

Он подвержен старению и требует применения громоздких поверочных схем. Современное развитие науки пока не позволяет с достаточной степенью точности связать килограмм с естественными атомными константами.

Единица температуры может быть получена
как производная с использованием уже введенных величин геометрии и механики на основании одного из четырех уравнений связи – как величина, пропорциональная:
1. произведению давления на объем одного моля газа –
из закона Менделеева-Клапейрона;

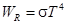
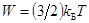
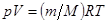2. кинетической энергии поступательного движения молекулы идеального газа;

3. объемной плотности электромагнитного излучения – из закона Стефана-Больцмана;

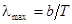4. длине волны такого излучения, на которую приходится максимум излучения – из закона Вина.

Здесь R – универсальная газовая постоянная,
k _Б – постоянная Больцмана,
s – постоянная Стефана-Больцмана

В термодинамике показано, что приведенные формулы определяют одну и ту же температуру, которая получила название термодинамической. Любой из коэффициентов
R, k _Б, s или l_max, используемых в формулах, можно было бы приравнять к единице. Это обеспечило бы разные размерности температуры как производной единицы.

Однако учёные посчитали целесообразным выделить температуру в ряд основных величин, что привело
к возникновению новой фундаментальной константы – постоянной Больцмана. Универсальная газовая постоянная, постоянные Стефана-Больцмана и Вина выражаются через постоянную Больцмана и другие константы.

Температура измеряется в кельвинах. Один кельвин равен 1/273,16 части термодинамической температуры тройной точки воды. Остальные тепловые единицы образуются на основании известных уравнений связи между ними и введенными ранее физическими величинами.

Дата добавления: 2014-01-06