Амплитуда волны, рассеянной ограниченным кристаллом

Связь формы узлов обратной решетки с величиной и габитусом кристалла

Учтем реальные размеры кристаллитов. Для этого введем понятие функции формы. Пусть функция 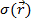обладает следующими свойствами: она равна единице внутри объекта и нулю вне объекта.

Если определяет распределение электронной плотности для неограниченного кристалла, то произведение определяет распределение электронной плотности в ограниченном кристалле-объекте.

Рис. К объяснению понятия функции формы.

Смоделируем тело следующим образом: тело состоит из N атомов, положение определяется векторами , 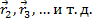Функции атомного рассеяния для атомов определены функциями f ₁, f ₂, f ₃,… амплитуда волны рассеянной всем объектом будет равна сумме N амплитуд когерентных волн, рассеянных всеми частицами объекта:

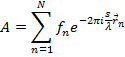
Исходной фазой является фаза волны, которая рассеивалась бы электроном, помещенным в начало координат пространства объекта.

Обобщим определение смоделированного объекта: введем функцию электронной плотности для данной точки , в таком случае амплитуда волны рассеянной объектом будет представляться интегралом по всему пространству объекта:

,

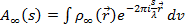т.е. функция есть Фурье преобразование функции . Если смоделированное твердое тело является кристаллом, тогда является тройной периодической функцией, значение будет равно нулю во всех точках обратного пространства за исключением узлов обратной решетки. В каждом узле обратной решетки эта функция принимает значение структурной амплитуды для этого узла hkl.

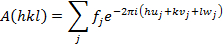
Вследствие существования побочных максимумов в уравнении Лауэ интенсивность дифракции отлична от нуля не только в точке самого узла hkl обратной решетки, но и в некоторой области, окружающей этот узел. Размеры этой области обратно пропорциональны размерам кристалла, т.е. дифрагируещего объекта.

Рассмотрим амплитуду волны, рассеянную объектом конечного размера. Для этого заменим в выражении амплитуды рассеянной волны функцию под знаком интеграла на произведение функций :

Как известно преобразование Фурье от произведения двух функций равно свертке преобразований Фурье от каждой функции:

,

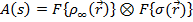где 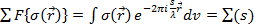- Фурье преобразование функции формы.

Для амплитуды волны, дифрагированной ограниченным кристаллом получим выражение:

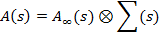
Эту формулу можно интерпретировать следующим образом: функция амплитуды дифрагированной волны от ограниченного кристалла является суперпозицией последовательных наложений Фурье-преобразования 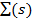на каждую точку обратного пространства умноженной на коэффициент, равный значению в соответствующей точке.

Дата добавления: 2014-01-07