Интенсивность волны, рассеянной ограниченным объектом

Обозначим через интенсивность волны, рассеянной объектом неограниченного размера

Введем новые переменные и :

Где введена функция , которая носит название обобщенной функции Паттерсона, которая равна самосвертке функции распределения электронной плотности в объекте. Полученная формула показывает, что функция J (s) в обратном пространстве является Фурье-образом функции , определенной в пространстве объекта.

Размеры объекта учтем через функцию формы :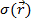

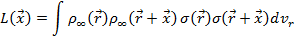
Произведение 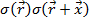равно 1, если точки и находятся внутри объекта, в противном случае это произведение равно 0 и функция 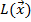также будет равна нулю.

Рассмотрим объем объекта внутри которого произведение 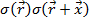равно 1. Обозначим его :

Геометрическая интерпретация, которого заключается в следующем: это есть объем общий для начального объема V и объема V(x), полученного в результате параллельного переноса на вектор х.

Рис. Геометрическая интерпретация функции

Интеграл, определяющий функцию 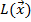равен:

Если вещество однородно, то функцию 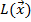можно представить как произведение среднего значения произведения электронных плотностей в веществе объекта на объем интегрирования :

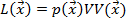
Интенсивность дефрагированных лучей представляется сверткой двух функций: функции, определяемой структурой объекта и функции определяемой его размером и формой.

Можно показать, что =, где 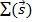- Фурье преобразование функции формы 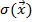. получила название «кристаллформфактора».

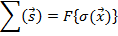
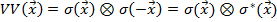
Свойства :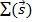

1) Если 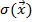действительно, тогда 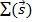- центрально-симметричная функция

2) Максимальное значение есть

3) Интеграл по объему пространства равен объему объекта в прямом пространстве V.

4) Функция настолько сжата или растянута в обратном пространстве насколько растянута или соответственно сжата функция 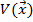в прямом пространстве.

Таким образом для объекта очень больших размеров функция имеет очень узкую область определения и наоборот для объекта маленького размера функция 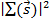растянута в обратном пространстве. В случае дифракции от ограниченного кристалла в обратном пространстве функция в некоторой области вокруг узла обратной решетки отлична от нуля, размеры и форма которой определяются размерами и формой объекта.

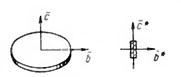
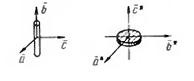
Рис. Примеры изменения формы областей обратного
пространства с изменением формы объекта

Литература

Е.К. Савицкая, Рентгеноструктурный анализ. Курс лекций

М.А. Порай-Кошиц, Основы структурного анализа химических соединений, Москва, Высшая школа 1989 (Глава 3)

Дата добавления: 2014-01-07