Типовые задачи оптимизации и их экономико-математические модели

Классическая задача оптимизации, решение методом множителей Лагранжа

Задача оптимального программирования, основные понятия и определения,

общая классификация. Примеры практических приложений

Определение 1. Задача оптимального программирования имеет вид:

Найти максимум или минимум функции
	(3.1)
при ограничениях
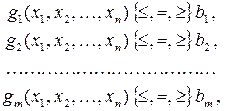
	(3.2)
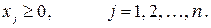
	(3.3)

f (X) – целевая функция (ЦФ), зависящая от вектора X;

Обозначение 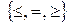говорит о том, что в каждом конкретном ограничении возможен один из этих знаков. Ограничения (3.1) называются функциональными ограничениями, а (3.2) – прямыми ограничениями.

Более компактно:

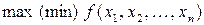
	(3.4)
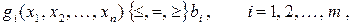
	(3.5)
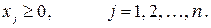
	(3.6)

Вектор X называется допустимым решением (допустимым планом задачи оптимального программирования), если его компоненты 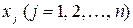удовлетворяют системе ограничений (3.4) и (3.5).

План 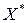называется оптимальным планом задачи оптимального программирования, если .

Определение 2. Решить задачу оптимального программирования – это значит:

1) найти оптимальный план ;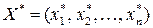

2) найти оптимальное значение .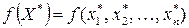

Задачи оптимального программирования классифицируют по следующим признакам:

· линейные и нелинейные задачи (по характеру связей между переменными);

· непрерывные и дискретные задачи (по характеру изменения переменных);

· статические и динамические задачи (по учету фактора времени);

· однокритериальные и многокритериальные задачи (по числу критериев оценки альтернатив);

· задачи в условиях полной определенности, в условиях неполной информации (случай риска) и в условиях неопределенности (по наличию информации о переменных).

Если в задаче оптимизации отсутствует условие неотрицательности переменных, а функциональные ограничения имеют вид равенств, то такую задачу называют классической задачей оптимизации:

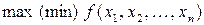
	(4.1)
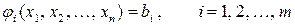.	(4.2)

Если все функции 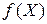, 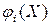непрерывны вместе с частными производными первого порядка, то для решения задачи оптимизации можно применить классический метод множителей Лагранжа.

Алгоритм:

1. Сначала составляют функцию Лагранжа:

.

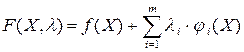(4.3)

2. Далее вычисляют для функции (4.3) частные производные первого порядка по всем переменным 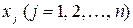и 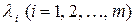, приравнивают их нулю и получают систему уравнений:

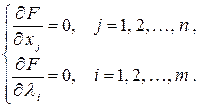
(4.4)

3. Если удается найти все решения системы (4.4), то для определения глобального максимума или минимума достаточно найти значения функции в соответствующих точках области определения задачи и выбрать наибольшее или наименьшее значение функции.

Замечание. Теоретической основой метода является следующее утверждение:

если функция f (X) в точке 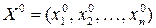имеет экстремум, то существует вектор 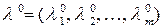такой, что точка 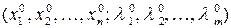является решением системы уравнений (4.4).

Задача об использовании ограниченных ресурсов.

Задача о размещении производственных заказов.

Задача о раскрое строительных материалов [1, с.30-31, 33-35].

Задача о смесях [1, с.37-38].

Задача об инвестициях [1, с.41-42, 45].

Задача о «ранце».

Задача о «рационе».

Задача о распределении рекламного бюджета.

Тема 2: Линейное программирование

Дата добавления: 2014-01-07