Методы сетевого планирования и управления

Классическая модель управления запасами с допущением дефицита

Классическая модель управления запасами без дефицита

Управление запасами (УЗ) – установление периодичности поставок, их объемов, регулярности и наилучших сроков выполнения.

Рассматривают несколько основных систем регулирования запасов:

· система с фиксированным размером заказа [1, с.123];

· система с фиксированной периодичностью заказа [1, с.124];

· система с двумя фиксированными уровнями или (s-S)-система [1, с.124];

· системы оптимального управления запасами [1, с.125] и т.д.

Разработаны различные модели управления запасами:

· детерминированные модели;

· стохастические модели;

· статические модели;

· динамические модели.

Простейшей моделью УЗ является классическая модель системы управления запасами наиболее экономичного размера партии (модель Уилсона). Это детерминированная модель, имеющая аналитическое решение. Она основана на выборе фиксированного размера заказываемой партии, которая минимизирует общие расходы на оформление заказа, доставку и хранение товара.

Предполагается также, что выполнены следующие условия:

· уровень запаса убывает равномерно от q до 0;

· время поставки заказа является известной и постоянной величиной;

· каждый заказ поставляется в виде одной партии; затраты s на оформление заказа и доставку товара не зависят от объема партии;

· ежедневная стоимость h хранения единицы товара постоянна;

· отсутствие запаса (дефицит) является недопустимым.

Циклы изменения уровня запаса в модели Уилсона графически представлены на рис.18.1. Максимальное количество продукции, которая находится в запасе, совпадает с размером заказа q.

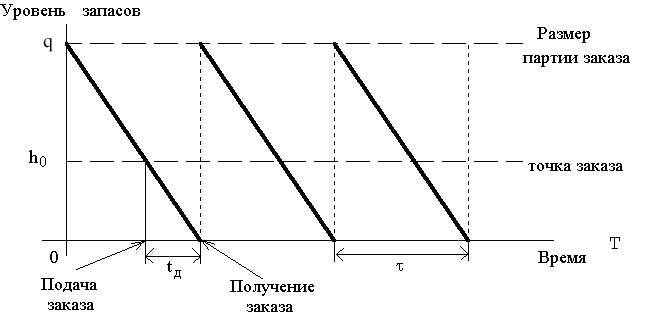
Рис.18.1. График циклов изменения запасов в модели Уилсона (без дефицита)

Входные параметры модели Уилсона

1) s – затраты на осуществление заказа, включающие оформление и доставку заказа и доставку товара (руб.);

2) 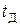– время доставки заказа (ед.вр.);

3) h – ежедневная стоимость хранения единицы товара (руб./ ед.тов.*ед.вр.);

4) l – спрос на товар за временной промежуток T (ед.тов.).

Выходные параметры модели Уилсона

1) q – размер заказа (ед.тов.);

2) t – период поставки, т.е. время между подачами заказа или между поставками (ед.вр.);

3) 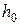– точка заказа, т.е. размер запаса на складе, при котором надо подавать заказ на доставку очередной партии (ед.тов.);

4) F – общие затраты на управление запасами (руб.).

Несложно вывести следующие формулы [1, с.128-129]:

1. Оптимальный размер заказываемой партии

.

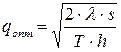2. Длительность цикла повторения заказа

.

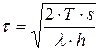3. Общее число партий, заказанных за временной промежуток T

.

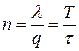4. Общая величина расходов

.

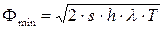Замечание. Минимум расходов имеет место в том и только в том случае, когда стоимость заказа равна расходам на хранение товара.

В некоторых случаях целесообразно ввести систему с плановым дефицитом, поскольку это приводит к уменьшению совокупных расходов на управление запасами.

Цикл изменения уровня запаса в модели Уилсона с допущением дефицита графически представлен на рис.19.1.

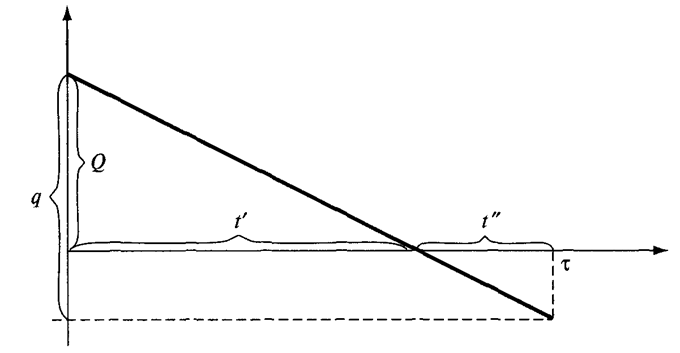
Рис.19.1. График цикла изменения запасов в модели Уилсона (с дефицитом)

Входные параметры модели Уилсона

1) s – затраты на осуществление заказа, включающие оформление и доставку заказа и доставку товара (руб.);

2) d – потери из-за дефицита, т.е. потери от нехватки единицы товара в единицу времени (руб./ ед.тов.*ед.вр.);

3) h – ежедневная стоимость хранения единицы товара (руб./ ед.тов.*ед.вр.);

4) l – спрос на товар за временной промежуток T (ед.тов.);

5) 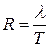– интенсивность спроса (ед.тов./ед.вр.).

Выходные параметры модели Уилсона

1) Q – уровень запаса в начале цикла движения запасов (ед.тов.);

2) t – период поставки, т.е. время между подачами заказа или между поставками (ед.вр.);

3) F – затраты на управление запасами в единицу времени (руб. /ед.вр.).

Расчет параметров модели [1, с.129-130]:

1. Оптимальный размер заказываемой партии

.

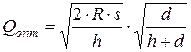2. Длительность цикла повторения заказа

.

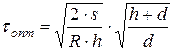3. Общая величина расходов

.

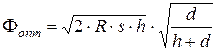Методы сетевого планирования и управления (СПУ) разработаны для обеспечения процесса планирования и выполнения работы как математические методы построения моделей исследования операций. Методы СПУ основаны на моделировании процессов с помощью сетевых графиков и представляют собой совокупность расчётных методов, организационных и контрольных мероприятий по планированию и управлению комплекса работ. К ним относятся методы, предназначенные для работы с сетевой моделью по временным, ресурсным, стоимостным и другим параметрам работ. Система СПУ позволяет:

· формировать календарный план реализации некоторого комплекса работ;

· выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы;

· осуществлять управление комплексом работ по принципу «ведущего звена» с прогнозированием и предупреждением возможных срывов в ходе работ;

· повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.

Рассмотрим метод критического пути (или СРМ – Critical Path Method), который был разработан в конце 50-х годов в США, в 1956 г., М. Уолкером из фирмы "Дюпон" и Д. Келли из группы планирования капитального строительства фирмы "Ремингтон Рэнд". Они попытались использовать ЭВМ для составления планов-графиков крупных комплексов работ по модернизации заводов фирмы "Дюпон".

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. При этом используются некоторые понятия, теоремы и обозначения теории графов (рис.20.1).

Основные понятия сетевой модели: событие, работа, путь.

Событие на графе отмечается кругом (с порядковым номером), является узловым пунктом сети.

Работа на графе отмечается стрелкой, соединяющая два события. Первое событие – конец предыдущей работы и начало предстоящей (рассматриваемой), второе событие – это окончание рассматриваемой работы. Действительная работа со своим объёмом затраченного времени, затратами ресурсов или ожидание обозначается сплошной стрелкой. Фиктивная работа (зависимость) – это пунктирная стрелка. Стрелки указывают последовательность выполнения операций. Взаимосвязь кружков и стрелок является графическими символами сетевой модели, которые должны строиться по определенным правилам.

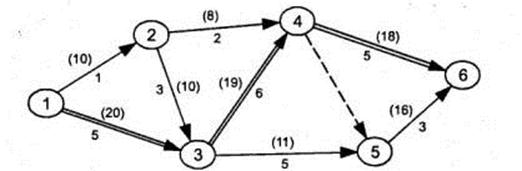
Рис.20.1. Схема сетевого графика

Начало стрелки показывает, с какого события данная работа начинается, а конец стрелки показывает, в каком событии она заканчивается. Работы имеют временные оценки, которые проставляются на стрелках. Событие считается свершившимся тогда, когда будет закончена самая длительная из всех входящих в него работ. Требуемые для выполнения работы размеры ресурсов указываются на стрелках в скобках.

Путем в графе называется такая упорядоченная последовательность дуг (стрелок), что конец любой дуги (стрелки), кроме последней, совпадает с началом следующей дуги.

Максимальный по продолжительности полный путь в сети называется критическим; работы, лежащие на этом пути, также называются критическими (на графике они отражаются двойными стрелками). Выявление критического пути позволяет установить работы (операции), определяющие ход выполнения проекта. Критические работы в ходе проектирования должны выполняться строго по графику. Именно длительность критического пути определяет наименьшую общую продолжительность работ по проекту в целом.

При анализе сетевого графика ставятся следующие задачи:

1. Отыскание минимального времени выполнения всего проекта (критического времени).

2. Отыскание тех операций, которые существенно влияют на критическое время; их совокупность образует так называемый критический путь.

Дата добавления: 2014-01-07