Основные оценочные параметры СК

Случайные колебания

Случайные колебания (СК) – это процесс при котором и амплитуда, и частота (фаза) изменяются по случайному характеру. Аналитическое описание такого процесса невозможно. Поэтому для их оценки прибегают к методам статистической радиотехники.

Рассмотрим случайный процессc S(t) (рис. 59).

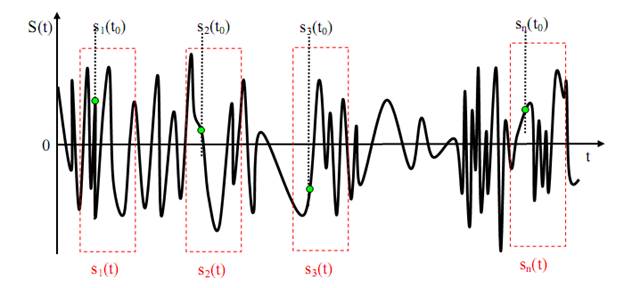
Рис. 59. Случайный процесс

При анализе данного процесса выделяются реализации s₁(t), s₂(t), s₃(t),... s_n(t) процесса S(t), представляющие собой фиксированные фрагменты процесса одинаковых отрезков времени.

Для оценки процесса в дискретный момент времени определяют сечение t₀. Если сечение проводится по ансамблю реализаций s₁(t₀), s₂(t₀), s₃(t₀),... s_n(t₀), то оно называется сечением процесса.

Достаточной характеристикой случайного процесса является плотность вероятности, которая определяется как частота попадания случайной величины в наперед заданный интервал этих величин (рис. 60)

Функция p(s) является дифференциальным законом распределения случайной величины S, а Р(s) есть интегральный закон распределения. При любом распределении должно выполняться так называемое правило нормировки:

Рис. 60. К определению плотности вероятности и правилу нормировки

Для оценки полученных реализаций определяют среднее значение (первый момент):

- для дискретной величины (по сечению)

- для непрерывной (по ансамблю реализаций)

Физически эта величина для электрического процесса имеет смысл постоянной составляющей. Единица измерения матожидания совпадает с единицей измерения случайной величины. На рис. 61 приведен пример матожидания для выбранной реализации. Как видно среднее значение несколько смещено относительно нулевого значения. Ясно, что с увеличением числа реализаций среднее будет определено более точно.

Определяют дисперсию (средний квадрат флуктуаций) как отклонение случайной величины от среднего значения (от матожидания):

- для дискретной величины

- для непрерывной

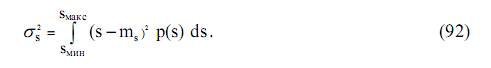
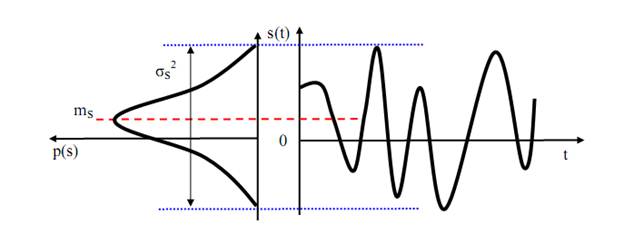
Рис. 61. Матожидание и дисперсия реализации СК

Дисперсия имеет размерность квадрата случайной величины. Для электропроцессов имеет смысл средней мощности (условно, приходящейся на сопротивление 1 Ом). Так как площадь подкривой распределения остается постоянной, то ясно, что при увеличении дисперсии кривая растягивается по оси случайных величин.

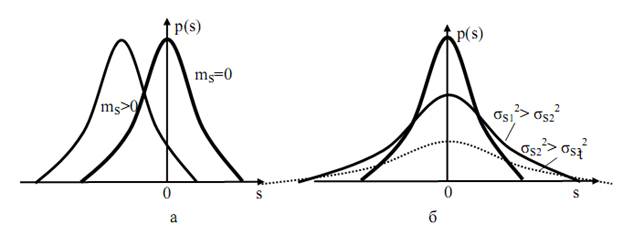
Рис. 62. Распределение плотности вероятности СК:

а – при различных матожиданиях; б – при различных дисперсиях

На рис. 62 приведены примеры распределения случайных величин при различных матожиданиях и дисперсиях.

Большинство случайных процессов подчиняются нормальному (гауссовому) закону распределения

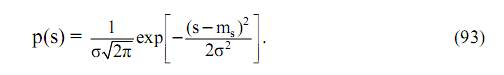
Дата добавления: 2014-01-07