Свойства автокорреляционной функции

Автокорреляционная функция обладает следующими основными свойствами:

1. при τ = 0 она максимальна и равна энергии сигнала, т.е.

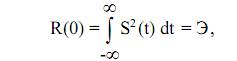
а при анализе СК его дисперсии;

2. является четной функцией

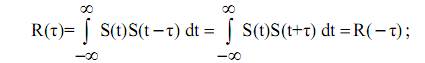
3. является убывающей функцией

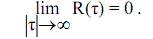
1.10.5. Свойства взаимной корреляционной функции

Взаимная корреляционная функция обладает следующими основными свойствами:

1. при τ = 0:

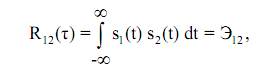
где Э₁₂ – взаимная энергия двух колебаний;

2. функция в общем случае не является четной функцией и необязательно достигает максимума при τ = 0;

3. является убывающей функцией – с ростом абсолютного значения τ колебаний с конечной энергией, она затухает;

4. обладает зеркальностью, т.е. если вместо задержки одного колебания рассматривать его опережение

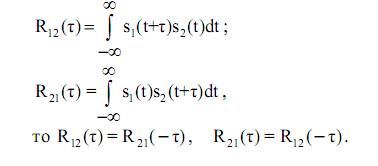
1.10.6. Связь энергетического спектра и автокорреляционной функция.

Теорема Винера-Хинчина

Определим взаимосвязь спектральной характеристики колебания и автокорреляционной функции, используя пару представления Фурье

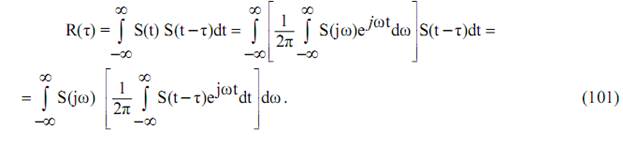
Выражение, входящее в квадратные скобки, согласно теореме смещения во времени, есть спектральная плотность домноженная на экспоненту јωτ

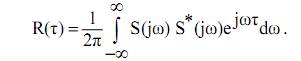
Перемножение комплексно-сопряженной функции есть квадрат модуля этой функции, поэтому

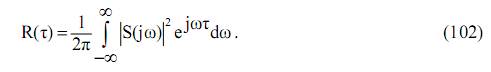
Сравнивая последнее выражение с обратным преобразованием Фурье, можно определить квадрат спектральной плотности как

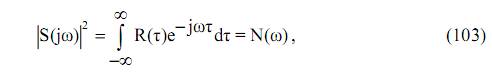
который по определению есть энергетический спектр СК.

Выражения (102)-(103) определяют суть теоремы Винера-Хинчина, которая утверждает, что энергетический спектр и автокорреляционная функция связаны между собой парой преобразования Фурье. Согласно этой теоремы можно сделать следующие заключения:

1) чем шире энергетический спектр СК, тем уже его автокорреляционная функция;

2) чем быстрее изменяется процесс во времени, тем больше он занимает места в частотной области, медленный процесс имеет более узкий энергетический спектр (рис. 67).

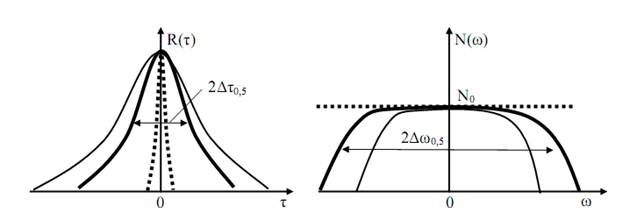
Рис. 67. Взаимосвязь корреляционной функции и спектральной

плотности мощности

Для оценки процесса с неопределенными временными параметрами применяют понятие интервала корреляции 2Δτ _0.5 , определяемый по половинному уровню корреляции относительно ее максимального значения. При этом связь с шириной энергетического спектра определяется как

Применяя аналогичные рассуждения в отношении двух, независимых друг от друга, колебаний можно ввести понятие взаимного энергетического спектра, определяемого выражением

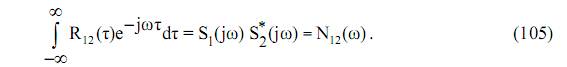
При решении ряда прикладных задач такое аналитическое введение является достаточно полезным.

Дата добавления: 2014-01-07