Броуновское движение (винеровский процесс). Белый шум

Пуассоновский процесс.

Введем теперь понятие нормального, или гауссовского, случайного процесса.

Определение. Случайный процесс , , называется нормальным или гауссовским, если для любых 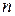моментов времени случайные величины имеют совместную гауссовскую плотность вероятности.

Наиболее распространенным дискретным марковским процессом является пуассоновский процесс. Он широко используется в теории массового обслуживания. Этим процессом описываются такие величины, как число фотонов, испускаемых веществом при радиоактивном распаде, число телефонных вызовов из данного района, число происшествий на данном перекрестке, число заявок на обслуживание и др.

Взвешенная в жидкости частица под действием молекулярного движения совершает хаотическое движение. Такое беспорядочное движение частицы было открыто Броуном. Эйнштейн установил, что средний квадрат отклонения частицы от ее первоначального положения за малый интервал времени (время столкновения) пропорционален этому интервалу, а именно

,

где – дисперсия отклонения частицы (средний квадрат отклонения ); – коэффициент диффузии.

В одномерном случае, когда частица за время перемещается на интервал 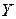только вдоль прямой (по оси ), последняя формула примет вид

.

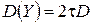Предположим, что перемещение 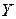распределено по нормальному (гауссовскому) закону и . Тогда можно записать

где 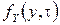– плотность распределения вероятностей случайного перемещения 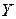частицы за время .

Если частица в отсчет времени пребывала в точке , то за 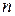шагов по оси частица получит приращения 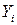, , 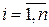соответствующие отсчетам времени 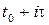, 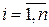. Будем считать приращения 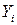, 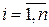независимыми и одинаково распределенными по нормальному закону. В момент времени эта частица будет иметь координату

Таким образом, имеем случайный процесс с дискретным временем. Полагая 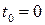, и выполняя замену переменной

, ,

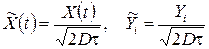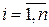получаем

,

где случайные величины 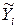независимы и имеют стандартное нормальное распределение , то есть , .

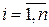Если предположить, что величина времени может быть сколь угодно малой, то при получим случайный процесс с непрерывным временем.

Пусть случайная координата регистрируется через интервалы времени 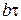, где – произвольное натуральное число. Можно показать, что в этом случае плотность распределения вероятностей перемещения 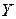определяется выражением

.

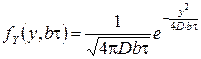Отсюда следует, что с увеличением шага, определяющего моменты наблюдения, приращения 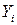координаты имеют нормальное распределение, эти приращения независимы и

, ,

где .

Поскольку по предположению может быть любой сколь угодно малой величиной, а величина 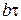– равной любому наперед заданному числу , то в соответствии с формулой (5.7.7) плотность вероятности координаты частицы имеет вид

, .

Отсюда для математического ожидания и дисперсии получаем следующие выражения:

, .

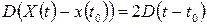В этих выражениях 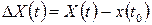есть приращение координаты за интервал времени . Таким образом, есть случайный процесс, определяющий броуновское движение. Случайная величина

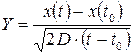
для любых действительных 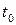и имеет стандартное нормальное распределение. Следовательно, для случайного процесса справедливо выражение

, ,

где случайная величина 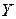имеет плотность вероятности .

Случайный процесс , определяемый последней формулой и описывающий броуновское движение, был введен Винером и называется винеровским процессом. Поскольку начало 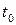случайного процесса выбрано произвольно, то любая траектория винеровского процесса с вероятностью 1 является непрерывной, но недифференцируемой функцией для всех .

Перед тем, как рассмотреть понятие белого шума, введем 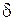- функцию Дирака (дельта-функцию). Иногда 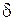- функцию Дирака определяют соотношением

,

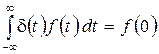где 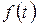– любая непрерывная в окрестности точки 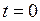функция. Однако с точки зрения классического анализа такая функция не может существовать. Поэтому 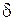- функцию в теории обобщенных функций рассматривают не как функцию, а как обобщенную функцию, то есть функционал , ставящий в соответствие каждой функции 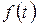, непрерывной в окрестности точки 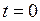, число .

Обобщенная функция определяется также как слабый предел дельтаобразной последовательности.

Определение. Последовательность обычных функций 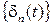называется дельтаобразной последовательностью, если для любой функции 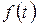, непрерывной в окрестности точки ,

.

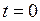Такой предел называют слабым пределом последовательности 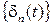и говорят, что последовательность 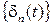слабо сходится к обобщенной функции .

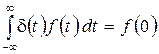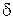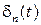Таким образом, формулу , определяющую - функцию, следует рассматривать как символическую запись выражения . Тогда элемент дельтаобразной последовательности при достаточно большом номере 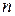является хорошим приближением обобщенной функции , что сближает понятия обычной и обобщенной функции.

Аналогично соотношением

вводится обобщенная функция .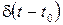

Можно доказать, что 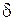- функция четна, то есть 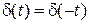, и представима интегралом Фурье:

.

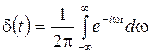Отсюда

.

Термин «белый шум» используется обычно для описания случайных флуктуаций, встречающихся в электронике и технике связи.

Определение. Стационарный процесс со спектральной плотностью , где 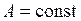, называется белым шумом.

Из определения следует, что белый шум имеет одинаковую плотность энергии на всех частотах 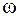. Поэтому по аналогии со светом такие процессы называются процессами типа белого шума.

Пусть – белый шум с непрерывным временем . Тогда его дисперсия равна

.

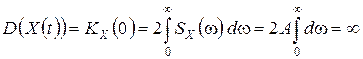Итак, для белого шума с непрерывным временем дисперсия бесконечна.

Найдем корреляционную функцию белого шума:

.

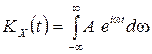Тогда

.

Отсюда

.

Следовательно, случайные величины и белого шума для любых моментов времен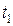и и , , являются некоррелированными.

Белый шум часто используется для моделирования случайных процессов, имеющих постоянную спектральную плотность в определенной полосе частот в тех случаях, когда несущественно поведение спектральной плотности вне интересующего диапазона частот. Некоррелированность значений белого шума в различные моменты времени – основная причина его широкого применения. Использование белого шума в теории случайных процессов во многом аналогично использованию 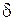- функции Дирака при анализе линейных систем.

Дата добавления: 2014-01-07