Квантили. Точные выборочные распределения.

Квантиль или 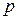- квантиль (100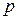-я процентиль) есть значение 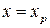случайной величины 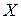, при котором

,

где – функция распределения случайной величины 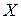. Вероятность 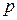называется порядком квантили .

Ясно, что - квантиль есть медиана 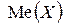. Квантил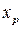и и называются симметричными. Если распределение симметрично относительно нуля, то 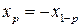. Применение квантилей согласно формуле (2.2.2) основывается на равенстве

.

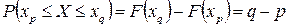Пусть 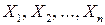– независимые нормально распределенные по закону 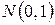случайные величины и . Закон распределения случайной величины называется распределением (хи-квадрат распределением) с степенями свободы или - распределением Пирсона.

Можно убедиться, что случайная величина имеет плотность вероятности

где 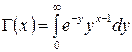– гамма-функция, обладающая следующими свойствами: , .

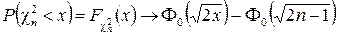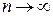Заметим, что при , где 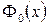– функция Лапласа.

Найдем математическое ожидание и дисперсию распределения . Для этого вычислим начальные моменты порядка 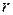. Имеем

.

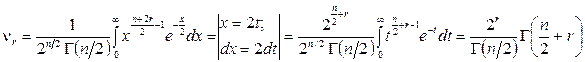Отсюда при 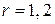получим соответственно

,

.

Тогда дисперсия равна .

Итак, для хи-квадрат распределения

; .

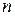Для - распределения с степенями свободы 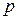- квантиль обозначается в виде 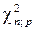. Например, квантиль означает выполнение равенства , а квантиль 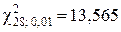– равенства .

Для нахождения 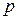- квантилей - распределения при 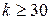применяют соотношения

,

,

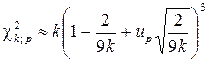где – 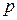- квантиль нормального распределения 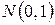. Первая из последних двух формул используется при , а вторая – применяется для вычисления квантилей 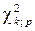малого порядка .

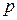Пусть и 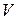– независимые случайные величины, причем – нормально распределенная случайная величина по закону 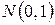, а 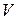имеет распределение с с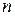тепенями свободы. Можно показать, что случайная величина имеет плотность вероятности

, .

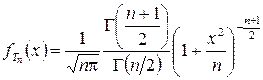Распределение вероятностей случайной величины 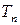с этой плотностью вероятности называется распределением Стьюдента с 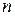степенями свободы или - распределением Стьюдента. Графики функции (6.6.4) называются кривыми Стьюдента. При любом . они симметричны относительно оси ординат, поэтому при любом 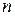математическое ожидание , и функция распределения 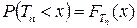удовлетворяет условию 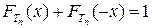. Дисперсия случайной величины 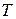равна 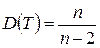. Можно показать, что при 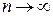плотность вероятности распределения Стьюдента сходится к плотности вероятности нормального распределения 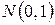, причем при распределение Стьюдента практически можно заменить нормальным распределением.

При для нахождения квантилей 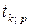можно воспользоваться формулой

.

После получения точечной оценки 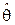параметра желательно иметь данные о надежности этой оценки, например, указать интервал , внутри которого с вероятностью 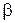находится точное значение параметра . Задачу получения такого интервала называют интервальным оцениванием, а сам интервал – доверительным.

Пусть задана случайная выборка случайной величины 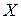с функцией распределения . Рассмотрим две статистики и 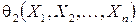такие, что для всевозможных реализаций случайной выборки выполняется неравенство 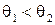, а для любых значений имеем

,

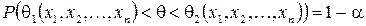то есть случайный интервал накрывает неизвестный параметр с вероятностью или в 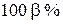случаев, которая не зависит от искомого параметра . Интервал называют доверительным интервалом для неизвестного параметра , вероятность – доверительной вероятностью или надежностью, с которой оцениваемый параметр покрывается интервалом , 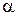– уровнем значимости. Границы 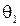и доверительного интервала 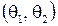называются доверительными. На практике обычно выбираются значения , что соответствует 90 –, 95 – и 99 %-ным доверительным интервалам соответственно. 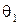Статистики и 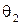обычно задают так, чтобы

.

В прикладных статистических задачах длина доверительного интервала играет важную роль: чем меньше его длина, тем точнее оценка. Если длина этого интервала велика, то ценность такой оценки незначительна.

Рассмотрим некоторые примеры, когда доверительный интервал может быть найден.

1. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Выведем формулу для вероятности попадания случайной величины, распределенной по нормальному закону , в данный интервал . Поскольку плотность распределения вероятностей нормально распределенной случайной величины 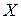есть

,

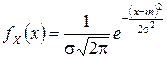а вероятность попадания случайной величины в интервал равна , то искомая вероятность

.

Вводя замены , , , получим

,

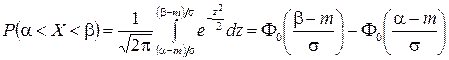где 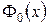– функция Лапласа.

В частности, если интервал симметричен относительно математического ожидания , то есть , то последняя формула в силу нечетности функции 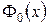приводится к виду

.

Положив в последней формуле и пользуясь таблицей 4 значений функции 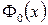, получаем

. ▲

Таким образом, с вероятностью 99,7 % значение нормально распределенной случайной величины отклоняется от математического ожидания не больше, чем на . Другими словами, в среднем в трех опытах из 1000 отклонение случайной величины 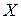от математического ожидания будет более . Поэтому областью практически возможных значений нормально распределенных случайных величин считается обычно интервал 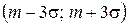. В этом и состоит «правило трех сигм».

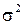2. Доверительный интервал для математического ожидания нормально распределенной генеральной совокупности при известной дисперсии. Пусть задана случайная выборка такая, что , распределены по нормальному закону , причем дисперсия известна. Найдем доверительный интервал для математического ожидания .

Случайная величина 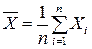имеет нормальное распределение . Рассмотрим случайную величину

.

Так как 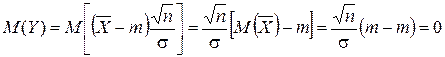и , то случайная величина имеет нормальное распределение 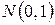. Следовательно,

,

где 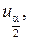– квантили нормального распределения .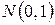

Это равенство можно также записать в виде

,

которое справедливо для любого значения случайной величины . Следовательно, для любой выборки интервал

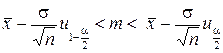
с доверительной вероятностью накрывает неизвестное математическое ожидание случайной величины .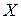

Нетрудно показать, что 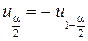, и тогда доверительный интервал можно записать в виде

.

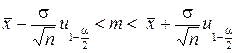Дата добавления: 2014-01-07