
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие статистической гипотезы
Интервальные оценки.
Лекция 24.
3. Доверительный интервал для математического ожидания нормально распределенной генеральной совокупности при неизвестной дисперсии. Пусть требуется оценить математическое ожидание генеральной совокупности, имеющей нормальное распределение 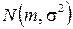 при неизвестной дисперсии
при неизвестной дисперсии 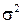 . В этом случае для построения доверительного интервала применяют статистику
. В этом случае для построения доверительного интервала применяют статистику 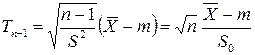 , где
, где 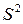 – случайное значение выборочной дисперсии, то есть
– случайное значение выборочной дисперсии, то есть 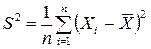 ;
; 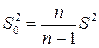 – случайное значение модифицированной (исправленной) выборочной дисперсия;
– случайное значение модифицированной (исправленной) выборочной дисперсия;  – случайная выборка такая, что случайные величины
– случайная выборка такая, что случайные величины 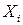 ,
, 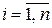 распределены по нормальному закону
распределены по нормальному закону 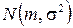 , в котором математическое ожидание
, в котором математическое ожидание 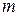 и дисперсия
и дисперсия 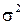 неизвестны.
неизвестны.
Можно показать, что случайная величина 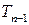 имеет распределение Стьюдента с
имеет распределение Стьюдента с  степенями свободы. Тогда
степенями свободы. Тогда
 ,
,
где  ,
, 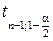 – квантили распределения Стьюдента.
– квантили распределения Стьюдента.
Отсюда находим доверительный интервал с уровнем значимости 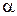 для математического ожидания
для математического ожидания 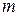 при неизвестной дисперсии
при неизвестной дисперсии 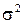 :
:
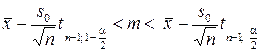 .
.
Если учесть, что 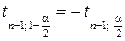 , то доверительный интервал можно записать в виде
, то доверительный интервал можно записать в виде
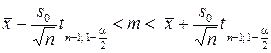 ,
,
где 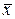 – выборочное среднее;
– выборочное среднее; 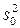 – модифицированная выборочная дисперсия;
– модифицированная выборочная дисперсия; 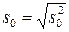 .
.
4. Доверительный интервал для дисперсии нормально распределенной генеральной совокупности при известном математическом ожидании. Найдем доверительный интервал для дисперсии 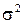 генеральной совокупности, имеющей нормальное распределение
генеральной совокупности, имеющей нормальное распределение 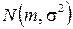 при известном математическом ожидании
при известном математическом ожидании 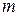 .
.
В этом случае для построения доверительного интервала применяют статистику 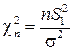 , где
, где 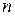 – объем случайной выборки
– объем случайной выборки  ;
; 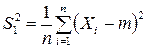 . Случайная величина
. Случайная величина 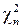 имеет
имеет 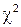 - распределение с
- распределение с 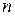 степенями свободы, и поэтому доверительный интервал находится из условия
степенями свободы, и поэтому доверительный интервал находится из условия
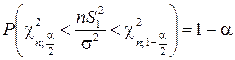 ,
,
где 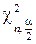 ,
, 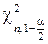 – квантили
– квантили 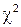 - распределения. Таким образом, для любой реализации
- распределения. Таким образом, для любой реализации 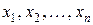 случайной выборки доверительный интервал
случайной выборки доверительный интервал
 ,
,
где 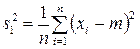 , накрывает с вероятностью
, накрывает с вероятностью 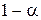 теоретическое значение дисперсии
теоретическое значение дисперсии 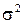 случайной величины
случайной величины 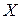 .
.
Извлекая квадратный корень из обеих сторон последнего неравенства, определяющего доверительный интервал для 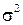 , получаем доверительный интервал для среднего квадратического отклонения
, получаем доверительный интервал для среднего квадратического отклонения 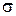 :
:
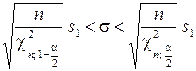 .
.
5. Доверительный интервал для дисперсии нормально распределенной генеральной совокупности при неизвестном математическом ожидании. В этом случае для построения доверительного интервала применяют статистику 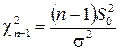 , где
, где 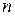 – объем случайной выборки
– объем случайной выборки  ;
; 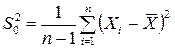 . Случайная величина
. Случайная величина 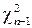 имеет
имеет 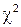 - распределение с
- распределение с  степенями свободы. Тогда
степенями свободы. Тогда
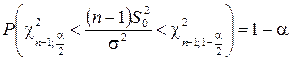 ,
,
где  ,
, 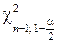 – квантили
– квантили 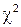 - распределения. Отсюда для любой реализации
- распределения. Отсюда для любой реализации 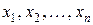 случайной выборки
случайной выборки  находим доверительный интервал
находим доверительный интервал
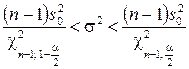
для дисперсии 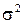 случайной величины
случайной величины 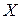 и доверительный интервал
и доверительный интервал
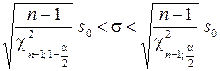
для среднего квадратического отклонения 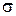 , где
, где 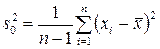 – модифицированная выборочная дисперсия;
– модифицированная выборочная дисперсия; 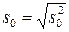 .
.
Статистическая гипотеза – это предположение относительно параметров или вида распределения случайной величины 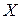 генеральной совокупности. Например, можно рассмотреть гипотезу о размерах изготовляемых деталей, об эффективности лекарства и т. д.
генеральной совокупности. Например, можно рассмотреть гипотезу о размерах изготовляемых деталей, об эффективности лекарства и т. д.
Гипотеза называется простой, если она однозначно определяет распределение случайной величины, в противном случае гипотеза называется сложной. Например, если предполагается, что случайная величина 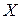 распределена по нормальному закону
распределена по нормальному закону  , то гипотеза
, то гипотеза 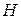 – простая, а если высказывается утверждение о нормальном распределении случайной величины с заданным параметром
– простая, а если высказывается утверждение о нормальном распределении случайной величины с заданным параметром 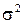 , но
, но 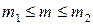 , то такая гипотеза – сложная.
, то такая гипотеза – сложная.
Правило, по которому принимается или отвергается гипотеза о значении параметра распределения случайной величины 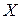 , называется критерием значимости. Если же распределение случайной величины
, называется критерием значимости. Если же распределение случайной величины 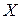 неизвестно и может быть высказана гипотеза о виде распределения этой случайной величины, то правило, с помощью которого принимают или отрицают данную гипотезу, называется критерием согласия. Процедура проверки гипотез – это процесс, позволяющий для любого значения
неизвестно и может быть высказана гипотеза о виде распределения этой случайной величины, то правило, с помощью которого принимают или отрицают данную гипотезу, называется критерием согласия. Процедура проверки гипотез – это процесс, позволяющий для любого значения 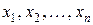 случайной выборки
случайной выборки 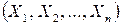 получить решение: принять или отклонить проверяемую гипотезу
получить решение: принять или отклонить проверяемую гипотезу 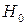 . Правило, согласно которому проверяется гипотеза
. Правило, согласно которому проверяется гипотеза 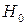 , называется статистической проверкой гипотезы
, называется статистической проверкой гипотезы 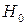 .
.
Гипотеза, подлежащая проверке, называется нулевой или основной и обозначается 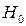 . Вместе с гипотезой
. Вместе с гипотезой 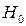 рассматривают одну из альтернативных (конкурирующих) гипотез
рассматривают одну из альтернативных (конкурирующих) гипотез 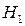 , заключающуюся в том, что если нулевая гипотеза отвергается, то принимается альтернативная. Например, если проверяется гипотеза о равенстве параметра
, заключающуюся в том, что если нулевая гипотеза отвергается, то принимается альтернативная. Например, если проверяется гипотеза о равенстве параметра 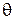 некоторому заданному значению
некоторому заданному значению 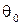 , то есть
, то есть 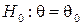 , то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез:
, то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: 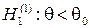 ,
, 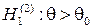 ,
, 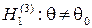 .
.
Статистическая проверка гипотезы основывается на том принципе, что маловероятные события считаются невозможными, а события с большой вероятностью считаются достоверными. Этот принцип реализуется следующим образом. Перед анализом выборки фиксируется уровень значимости 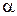 – вероятность ошибочного отклонения нулевой гипотезы. Обычно задаются значениями
– вероятность ошибочного отклонения нулевой гипотезы. Обычно задаются значениями 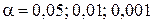 .
.
Для выбора критерия значимости выбирают подходящую статистику 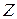 , которая обычно совпадает с интервальной статистикой параметра
, которая обычно совпадает с интервальной статистикой параметра 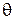 . Пусть
. Пусть 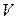 – множество значений статистики
– множество значений статистики 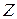 , а
, а 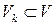 – такое подмножество множества
– такое подмножество множества 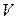 , что
, что 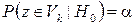 , то есть вероятность попадания значений
, то есть вероятность попадания значений 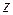 статистики
статистики 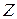 в область
в область 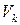 , при условии справедливости гипотезы
, при условии справедливости гипотезы 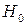 , равна уровню значимости
, равна уровню значимости 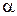 . Если
. Если  есть выборочное значение статистики
есть выборочное значение статистики 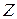 , вычисленное по выборке наблюдений, то критерий значимости можно сформулировать следующим образом: если
, вычисленное по выборке наблюдений, то критерий значимости можно сформулировать следующим образом: если 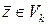 , то отклонить гипотезу
, то отклонить гипотезу 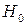 , если же
, если же 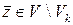 , то принять гипотезу
, то принять гипотезу 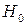 . Множество
. Множество 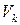 всех значений
всех значений  статистики
статистики 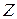 , при которых принимается решение, отклоняющее гипотезу
, при которых принимается решение, отклоняющее гипотезу 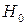 и принимающее гипотезу
и принимающее гипотезу 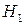 , называется критической областью. Совокупность же
, называется критической областью. Совокупность же 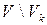 значений
значений  статистики
статистики 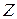 , при которых принимают гипотезу
, при которых принимают гипотезу 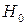 , называется областью принятия гипотезы. Точки, отделяющие критическую область от области принятия решений, называются критическими.
, называется областью принятия гипотезы. Точки, отделяющие критическую область от области принятия решений, называются критическими.
Таким образом, для определения критической области статистики используют уровень значимости 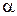 и учитывают вид альтернативной гипотезы
и учитывают вид альтернативной гипотезы 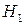 . Уровень значимости
. Уровень значимости 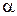 определяет «размер» критической области
определяет «размер» критической области 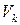 , а расположение критической области на множестве значений статистики
, а расположение критической области на множестве значений статистики 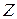 зависит от формулировки альтернативной гипотезы
зависит от формулировки альтернативной гипотезы 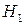 . Если проверяется гипотеза
. Если проверяется гипотеза 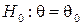 , то в случае альтернативной гипотезы
, то в случае альтернативной гипотезы 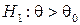 (
(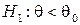 ) критическая область расположена на правом (левом) «хвосте» распределения статистики
) критическая область расположена на правом (левом) «хвосте» распределения статистики 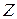 , то есть для заданного уровня значимости
, то есть для заданного уровня значимости 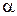 критическая область задается неравенством
критическая область задается неравенством 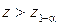 (
(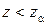 ), где
), где 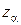 ,
, 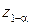 – квантили распределения статистики
– квантили распределения статистики 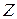 при условии, что верна гипотеза
при условии, что верна гипотеза 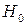 . Такие критерии называются односторонними (правосторонними и левосторонними). Если для гипотезы
. Такие критерии называются односторонними (правосторонними и левосторонними). Если для гипотезы 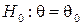 формулируется альтернативная гипотеза
формулируется альтернативная гипотеза 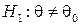 , то критическая область расположена на обоих «хвостах» распределения статистики
, то критическая область расположена на обоих «хвостах» распределения статистики 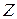 , то есть критическая область определяется неравенствами
, то есть критическая область определяется неравенствами 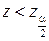 и
и 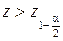 . В этом случае критерий значимости называется двусторонним.
. В этом случае критерий значимости называется двусторонним.
Принимая или отклоняя гипотезу 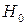 , можно допустить ошибки двух родов: 1) ошибка первого рода имеет место тогда, когда отвергается гипотеза
, можно допустить ошибки двух родов: 1) ошибка первого рода имеет место тогда, когда отвергается гипотеза 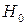 , в то время как в действительности она верна; 2) при ошибке второго рода принимается гипотеза
, в то время как в действительности она верна; 2) при ошибке второго рода принимается гипотеза 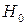 , в то время как верна на самом деле одна из альтернативных гипотез
, в то время как верна на самом деле одна из альтернативных гипотез 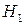 .
.
Пусть 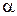 – вероятность ошибки первого рода, а
– вероятность ошибки первого рода, а 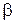 – вероятность ошибки второго рода. Тогда можно сказать, что при большом количестве выборок доля ложных заключений равна
– вероятность ошибки второго рода. Тогда можно сказать, что при большом количестве выборок доля ложных заключений равна 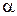 , если верна гипотеза
, если верна гипотеза 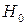 , и равна
, и равна 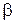 , если верна гипотеза
, если верна гипотеза 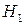 . Например, в радиолокации принято, что гипотеза
. Например, в радиолокации принято, что гипотеза 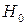 – отсутствие цели, а гипотеза
– отсутствие цели, а гипотеза 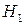 – наличие цели. Тогда принятие гипотезы
– наличие цели. Тогда принятие гипотезы 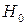 , когда на самом деле верна гипотеза
, когда на самом деле верна гипотеза 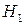 , называют пропуском сигнала, а вероятность принятия такого решения называется вероятностью пропуска
, называют пропуском сигнала, а вероятность принятия такого решения называется вероятностью пропуска 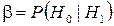 . Величина
. Величина 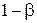 называется вероятностью правильного обнаружения. Принятие гипотезы
называется вероятностью правильного обнаружения. Принятие гипотезы 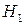 , то есть решение о том, что цель присутствует, когда эта гипотеза несправедлива и цели в действительности нет, называется вероятностью ложной тревоги
, то есть решение о том, что цель присутствует, когда эта гипотеза несправедлива и цели в действительности нет, называется вероятностью ложной тревоги 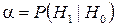 .
.
Предположим, что рассматриваются основная 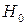 и альтернативная
и альтернативная 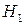 гипотезы. Тогда ошибки первого и второго рода можно изобразить в виде следующей таблицы:
гипотезы. Тогда ошибки первого и второго рода можно изобразить в виде следующей таблицы:
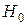 верна верна
| 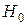 не верна не верна
| |
Отвергнуть 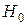
| Ошибка первого рода
с вероятностью 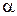
| Верное решение
с вероятностью 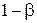
|
Принять 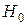
| Верное решение
с вероятностью 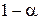
| Ошибка второго рода
с вероятностью 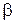
|
Статистическая проверка гипотезы состоит из следующих этапов:
1) формулировка нулевой 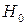 и альтернативной
и альтернативной 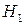 гипотез;
гипотез;
2) выбор соответствующего уровня значимости 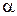 ;
;
3) определение объема выборки 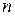 ;
;
4) выбор статистики 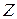 критерия значимости или согласия для проверки гипотезы
критерия значимости или согласия для проверки гипотезы 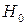 ;
;
5) определение (по таблицам, по уровню значимости 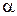 и по альтернативной гипотезе
и по альтернативной гипотезе 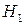 ) критической области и области принятия гипотезы;
) критической области и области принятия гипотезы;
6) формулировка правила проверки гипотезы;
7) принятие статистического решения: если значения статистики не входит в критическую область, то принимается гипотеза 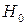 и отвергается гипотеза
и отвергается гипотеза 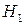 , а если входит в критическую область, то отвергается гипотеза
, а если входит в критическую область, то отвергается гипотеза 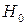 и принимается
и принимается 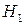 .
.
Результаты проверки статистической гипотезы нужно интерпретировать так: если приняли гипотезу 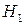 , то можно считать ее доказанной, а если приняли гипотезу
, то можно считать ее доказанной, а если приняли гипотезу 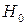 , то признали, что гипотеза
, то признали, что гипотеза 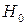 не противоречит результатам наблюдений. Однако этим свойством наряду с
не противоречит результатам наблюдений. Однако этим свойством наряду с 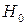 могут обладать и другие гипотезы. Принимая гипотезу
могут обладать и другие гипотезы. Принимая гипотезу 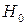 , следует проводить еще дополнительные исследования.
, следует проводить еще дополнительные исследования.
|
|
Дата добавления: 2014-01-07; Просмотров: 838; Нарушение авторских прав?; Мы поможем в написании вашей работы!