Властивості визначників

1. Визначник з нульовим рядком або стовпчиком дорівнює нулю.

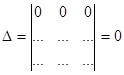Доведення. Оскільки за озн.1 в кожному доданку є множник з цього нульового рядка, то кожний доданок дорівнюватиме нулю, і 0+0+...+0=0.

2. Спільний множник можна виносити з рядочка чи стовпчика визначника і записувати його перед визначником.

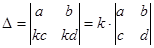Доведення. В кожному добутку є по одному елементу з даного рядка, і спільний множник k можна винести за дужку: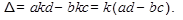

3. Якщо у визначнику поміняти місцями два рядки або стовпці, то він змінить знак на протилежний.

.

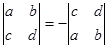Доведення. Очевидно, що добутки елементів будуть такі ж. При перестановці двох елементів перестановка змінює парність, тому всі добутки змінять знак.

4. Якщо у визначнику поміняти місцями рядки і стовпці, не змінюючи їх порядку (такий процес називається транспонуванням), то значення визначника не зміниться.

.

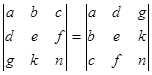Доведення. В усіх добутках тепер другі індекси будуть утворювати натуральну перестановку. Із третьої властивості перестановок випливає, що якщо переставляти елементи так щоб перші індекси були в порядку зростання, то другі індекси утворять перестановку такої ж парності, якою була перша.

Після цієї властивості зрозуміло, що всі властивості, які мають місце для рядків є справедливими і для стовпців, бо при транспонуванні одні переходять в інші, а значення визначника не змінюється.

і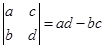

5. Якщо у визначнику є два однакові рядки або стовпці, то він дорівнює нулю.

Доведення. Поміняємо місцями ці рядки. За властивістю 3 зміниться знак: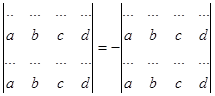

a -a

a = -a 2a=0 a=0.

6. Якщо у визначнику є два пропорційні рядки (стовпці), то він дорівнює нулю.

Доведення. .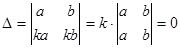

7. Якщо у визначнику в якомусь рядку (стовпці) всі елементи є сумами двох чисел, то визначник дорівнює сумі двох визначників. В першому з них в цьому рядку є тільки перші доданки, а у другому – другі. Всі інші рядки такі як в початковому визначнику:

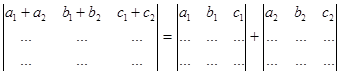. Доведення. В кожному добутку буде по одному множнику-сумі з даного рядка. Далі розкриємо дужки і погрупуємо добутки в яких є елемент з індексом 1 в перший визначник, а з індексом 2 – в другий.

8. При додаванні до елементів рядка відповідних елементів іншого рядка, помножених на одне і те ж число, значення визначника не зміниться. При цьому в таблиці визначника зміниться тільки рядок, до якого додаємо.

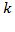
. Доведення. .

Дана властивість дуже важлива. Користуючись нею спрощують визначник, перетворюючи в деякому рядку (ст.) всі елементи крім одного в нулі.

-3

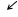
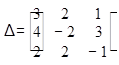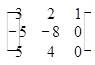Приклад. = == 0-20+0+40-0-0=20.

Означення 2. Якщо викреслити рядок і стовпчик у визначнику, у якому стоїть елемент a_ij (i-тий рядок, j-тий стовпчик), то отриманий визначник називаємо доповнювальним мінором М_ij до елемента a_ij.

Приклад.

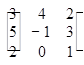M₃₂= , M₂₂=.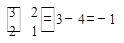

Означення 3. Алгебраїчним доповненням до елемента a_ij називається число, що обчислюється за формулою: A_ij=M_ij(-1)^i+j

Отже, A_ij та M_ij рівні або відрізняються знаком.

Приклад. M₃₂=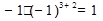, M₂₂=.

Зауваження. Якщо розкрити визначник A₁₁=М₁₁ і помножити на а₁₁, то отримаємо всі доданки початкового визначника з елементом а₁₁. (Всі знаки збережуться, бо якщо з перестановки забрати перший елемент 1, то кількість інверсій і парність не зміниться). Аналогічно, розкривши дужки у виразі a_ijA_ij отримаємо всі доданки початкового визначника з елементом a_ij. (Можна переставити і-тий рядок на місце першого рядка, поступово його піднімаючи (буде і-1 перестановок, тобто і-1 змін знаків всіх добутків), та аналогічно переставити j-тий стовпець на місце першого (j-1 змін знаків). Разом i+j-2 змін знаків, можна вважати i+j. Тепер елемент a_ij на місці а₁₁, а мінор М_ij на місці А₁₁, тому всі добутки мають потрібні знаки.)

Із зауваження випливає наступна властивість.

9. Властивість Лапласа: розклад визначника за елементами рядка чи стовпчика.

=a₁₁A₁₁+a₁₂A₁₂+a₁₃A₁₃

Визначник дорівнює сумі добутків елементів одного рядка (стовпчика) на відповідні алгебраїчні доповнення.

Вправа. Довести властивість для першого рядка визначників 2-го і 3-го порядків, розписавши алгебраїчні доповнення за означенням.

Пр. .

; ;.

Дана властивість дозволяє заміняти визначник на суму визначників нижчих порядків. Використавши її потрібну кількість разів, зведемо визначник будь-якого порядку до визначників 3-го чи 2-го порядків, які ми вміємо обчислювати точно.

Для того щоб обчислювати менше алгебраїчних доповнень спочатку за властивістю 8 добре було б зробити в одному рядку (ст.) всі елементи крім одного нулями.

-2

Пр. =.

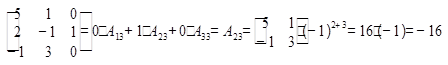Зауваження. Сума добутків b₁A_i1+b₂A_i2+b₃A_i3 , де b₁, b₂, b₃ -- деякі числа, дорівнює зміненому початковому визначнику, в якому на місці і-того рядка стоять числа b₁, b₂, b₃.

10. Сума добутків елементів одного рядка на алгебраїчні доповнення до відповідних елементів іншого рядка дорівнює нулю.

. Наприклад, a₃₁A₁₁+a₃₂A₁₂+a₃₃A₁₃=0.

Доведення. Дана сума добутків є за властивістю Лапласа розкладом за першим рядком такого визначника, в якого на місці першого рядка стоять елементи третього рядка:

= 0, бо є однакові рядки.

Дата добавления: 2014-01-06