Продовження дослідження лінійного простору

Нехай в просторі є ненульовий елемент х₁. Тоді він лінійно незалежний. Будемо добавляти до нього поступово елементи простору, стараючись, щоб сукупність залишалась лінійно незалежною. Можливі два випадки:

1) існують лінійно незалежні сукупності з нескінченною кількістю елементів.

2) всі незалежні сукупності мають скінченну кількість елементів.

Ми будемо працювати з просторами, де виконується умова 2.

Властивість 1. Нехай х₁, х₂, … х_n – максимальна сукупність лінійно незалежних елементів. Тоді будь-який елемент простору лінійно виражається через х₁, х₂, … х_n однозначно.

Доведення. Добавимо до цієї сукупності х - будь-який елемент простору. Тоді система

х₁, х₂, … х_n, х – лінійно залежна. Тобто існують не всі нульові коефіцієнти 𝜆₁, 𝜆₂,…, 𝜆_n, 𝜆_n+1, що виконується рівність: 𝜆₁×х₁ +𝜆₂×х₂+…+𝜆_n×х_n + 𝜆_n+1 х = 0.

𝜆_n+1¹0, бо інакше х₁, х₂, … х_n – лінійно залежні. Тому х можна виразити через інші елементи, перенісши їх вправо і поділивши на 𝜆_n+1.

Доведемо однозначність розкладу. Нехай х=а₁×х₁ +а₂×х₂+…+а_n×х_n та х= с₁×х₁ +с₂×х₂+…+с_n×х_n.

Прирівняємо, перенесемо вправо та зведемо подібні доданки:

(а₁-с₁₎×х₁ +(а₂-с₂)×х₂+…+(а_n-с_n)×х_n=0. Всі коефіцієнти повинні бути нулями через лінійну незалежність х₁, х₂, … х_n, отже, а_і = с_і, для всіх і=.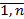

Властивість 2. Всі максимальні лінійно незалежні системи мають однакову кількість елементів.

Доведення. Нехай х₁, х₂, … х_n та у₁, у₂, … у_m – дві максимальні лінійно незалежні системи. Припустимо, що m>n. Будь-який елемент виражається через х₁, х₂, … х_n отже у₁, у₂, … у_m також.

у₁= а₁₁×х₁ +а₁₂×х₂+…+а_1n×х_n | c₁

у₂= а₂₁×х₁ +а₂₂×х₂+…+а_2n×х_n | c₂

_…

у_m= а_m1×х₁ +а_m2×х₂+…+а_mn×х_n | c_m

Складемо лінійну комбінацію у₁, у₂, … у_m і прирівняємо її до нуля:

с₁×у₁ +с₂×у₂+…+с_m×у_m = 0.

Підставимо попередні розклади погрупуємо подібні доданки. Отримаємо рівність деякої комбінації елементів х₁, х₂, … х_n нулю. Оскільки вони лінійно незалежні, то всі коефіцієнти лінійної комбінації рівні нулю. Отримали систему рівнянь для коефіцієнтів с₁,с₂,…с_m:

а₁₁×с₁ +а₂₁×с₂+…+а_m1×с_m = 0

а₁₂×с₁ +а₂₂×с₂+…+а_m2×с_m = 0

_…

а_1n×с₁ +а_2n×с₂+…+а_mn×с_m = 0

Ця система однорідна, кількість рівнянь (n) менша ніж кількість невідомих (m). Отже, вона має безліч розв’язків, тому має і ненульовий розв’язок. Тобто існують не всі нульові коефіцієнти с₁,с₂,…с_m, при яких лінійна комбінація елементів у₁, у₂,…у_m дорівнює нулю. Суперечність, бо у₁, у₂,…у_m лінійно незалежні. Отже, n=m.

Означення. Базис (синонім – основа).

Базисом чи фундаментальною сукупністю елементів лінійного простору V - називається така сукупність його об’єктів через які о д н о з н а ч н о можна виразити будь-який об’єкт лінійного простору з допомогою дій додавання та множення на число. Кількість елементів у базисі називається розмірністю простору. Позначається dimV.

Вправа. Довести, що елементи базису лінійно незалежні. (Тому що нульовий елемент теж повинен отримуватися єдиним способом, тобто тільки коли всі коефіцієнти .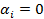

Базис – це також максимальна система лінійно незалежних елементів простору.

Зауваження. dimV =n. Нехай є деякий базис простору. Кожному елементу простору можна поставити у відповідність набір (n-елементний рядок) його коефіцієнтів при розкладі за цим базисом. Їх називають координатами елемента в даному базисі. Ця відповідність взаємно однозначна (чому?). Тоді лінійні операції об’єктів зводяться до таких операцій з n-елементними рядками.

Приклад (одновимірного простору). (2;4;5) – рядок – базис. Тоді лінійний простір

V= {(2z;4z;5z), z є ℝ} буде одновимірним.

Приклад. Простір n-елементних рядків (стовпців) є n- вимірним простором, бо можна вказати один з його базисів:

e₁= (1;0;0;…;0;0),

e₂= (0;1;0;…;0;0),

…

e_n= (0;0;0;…;0;1).

Тут n елементів. Будь-який елемент 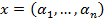виражається через них однозначно:

.

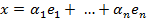Базис розв’язків однорідної системи частіше називають фундаментальною системою розв’язків цієї системи.

Приклад 1. Знайти всі розв’язки і фундаментальну систему розв’язків однорідної системи

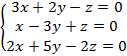
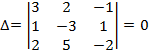
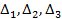теж рівні 0 (бо є нульовий стовпчик). Буде безліч розв’язків. Пошукаємо залежне рівняння: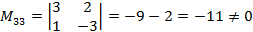

Можна викреслити третє рівняння.

=>

;

;

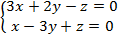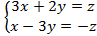
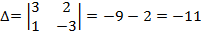
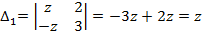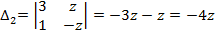
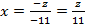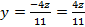
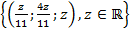– простір розв’язків.

Пошукаємо фундаментальну систему розв’язків. .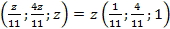

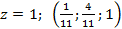– фундаментальна система розв’язків (ФСР), тому що всі інші розв’язки можна отримати з цього одного єдиним способом, помноживши його на відповідне число z. (Простір розв’язків – одновимірний).

Відповідь. 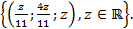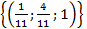— ФСР.

Приклад 2.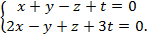

,

.

.

=

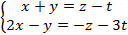
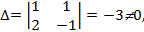
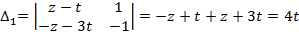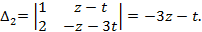
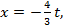
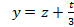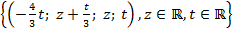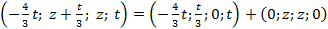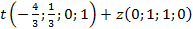
Отже, ФСР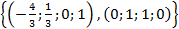

Відповідь. 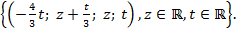ФСР:

Тепер очевидним є алгоритм знаходження ФСР якщо відомий загальний розв’язок однорідної системи: Нехай є деяка кількість вільних невідомих t,z,s,…,p. Потрібно надати їм таких значень t=1, z=0,s=0,…,p=0; t=0, z=1,s=0,…,p=0; … t=0, z=0,s=0,…,p=1.

Тоді отримані розв’язки складуть ФСР (бо через них можна виразити будь-який розв’язок системи однозначно).

Отже, кількість вільних невідомих буде розмірністю простору розв’язків однорідної системи.

Зауваження. Якщо 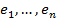– базис (фундаментальна система), то 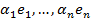– теж, де

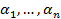– всі ненульові числа. (Довести.)

Тому в останньому прикладі можна записати ФСР з цілочисельними координатами:

ФСР: .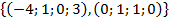

Дата добавления: 2014-01-06