Квадратичні форми і скалярний добуток

Далі будемо працювати в n вимірному евклідовому просторі .

Означення 28.16. (Друге означення евклідового простору).

Евклідів простір це дійсний векторний простір ‹_n, на якому задана додатньо визначена квадратична форма 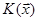. Доведемо еквівалентність означення 28.16 і 2.5.

◄ Нехай має місце означення 2.5. Виберемо в якості симетричної білінійної форми З аксіом 1-3 випливає, що це саме симетрична білінійна форма, а з аксіом 4 випливає, що квадратична форма додатньо визначена.

Нехай має місце означення 28.16.Поновимо за співвідношенням (28.5) симетричну білінійну форму, яка породила дану квадратичну. Введемо в ‹_n скалярний добуток за формулою 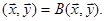Аксіоми 2, 3 виконуються, так як В – білінійна форма. Аксіома 1 виконується, оскільки В – симетрична. Аксіома 4 виконується, так як - додатньо визначена. ►

Зауваження 28.11. Так як , то ввівши базис в маємо

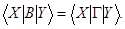Користуючись саме тим, що матриці Х, У можуть бути довільними, маємо В = Г.

Зауваження 28.12. З доведення еквівалентності означень 28.16 і 2.5 випливає, що додатня визначеність квадратичної форми потрібна тільки для виконання аксіоми 4 означення 2.5. Розглядаються простори, в яких скалярний добуток задається довільною квадратичною формою. В таких просторах існують вектори з від’ємним скалярним квадратом і геометрія значно відрізняється від евклідової. Якщо скалярний добуток означений квадратичною формою рангу, рівного розмірності простора, то такий простір має назву псевдоевклідового.

Теорема 28.5. (Критерій Сільвестра). Для додатньої визначеності квадратичної форми необхідно і достатньо, щоб головні мінори її матриці В задовольняли нерівностям

.

◄ Необхідність. Нехай на!!! задана додатньо визначена квадратична форма 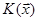. Введемо в!!! скалярний добуток з допомогою цієї квадратичної форми. Тоді матриця В буде матрицею Грама базису 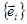. Головний мінор матриці В буде матрицею Грама лінійно незалежної системи базисних векторів 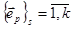. і за теоремою 2.3 її визначник більший за нуль.

Достатність. Доведення достатності проведемо індукцією по розмірності простору.

1) При n=1 достатність умови очевидна.

2) Припустимо, що вона має місце для просторів розмірності n-1.

3) Доведемо, що ці умови достатні і для просторів розмірності n. Запишемо 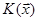, виділивши члени, які містять :

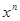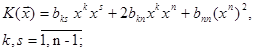без сумування по n.

Перша сума в правій частині останньої нерівності є квадратична форма К* задана в просторі розмірності n-1. Всі головні мінори матриці К* будуть головними мінорами матриці К і тому додатними. У відповідності до припущень індукції можна перейти до нового базису , в якому квадратична форма К* буде мати канонічний вигляд з усіма коефіцієнтами +1

К*=.

В новому базисі маємо

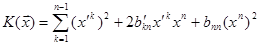
(без сумування по n).

Перетворимо цей вираз:

Введемо ще один базис 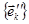, в якому 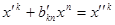і позначимо Тоді маємо (28.9)

Легко бачити, такі нові базиси можна ввести.

Відмітимо, що при заміні базису визначник матриці квадратичної форми не міняє знак, тому що згідно (28.4) і теореми про добуток визначників, він множиться на квадрат визначника матриці переходу Т. В вихідному базисі 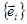визначник матриці квадратичної форми Л додатній, так як це головний мінор порядку n. В новому базисі цей визначник дорівнює . Звідси випливає нерівність Тепер з (28.9) видно, що квадратична форма 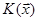додатньо визначена ►.

Означення 28.17. Лінійний оператор А в евклідовому просторі називається приєднаним до квадратичної форми К, якщо

1) А – самоспряжений (А = А* або

2)

Твердження 28.7. Кожна квадратична форма, задана на , має єдиний приєднаний лінійний оператор.

◄ Оберемо в довільний базис. Г-матриця Грама цього базису. Тоді з означення 28.7 для будь-якої матриці Х – координат вектора маємо

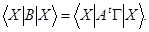
Зважаючи на те, що матриця Х – будь-яка, маємо

(28.10)

В ортонормованому базисі Г = Е, А = А^Т і тому

А = В. (28.10 а)

Шуканий лінійний оператор задається матрицею, яка задовольняє співвідношення (28.10), а в ортонормованому базисі (28.10а).

Для доведення єдності приєднаного до квадратичної форми лінійного оператора припустимо, що для даної квадратичної форми існує два таких лінійних оператора. Але тоді згідно (28.10) їх матриці (і, відповідно, оператори) співпадуть ►.

Теорема 28.6. В евклідовому просторі для кожної квадратичної форми існує ортонормований базис, в якому вона має діагональний вигляд.

◄ Приєднаний лінійний оператор – самоспряжений, а для самоспряжених операторів завжди існує ортонормований базис, який складається з власних векторів цього оператора, а в базисі власних векторів матриця оператора А і, відповідно, матриця В буде мати діагональний вигляд ►.

Зауваження 28.14. В базисі, який розглядається, по діагоналі матриці В будуть стояти власні числа оператора А.

Теорема 28.7. Нехай в векторному просторі ‹_n задані дві квадратичні форми К і , причому - додатньо визначена. Тоді в ‹_n існує базис, в якому обидві форми мають діагональний вигляд (а форма має навіть канонічний вигляд).

◄ Для доведення введемо в ‹_n скалярний добуток за допомогою додатньо визначеної квадратичної форми . По відношенню до цього скалярного добутку ортонормованими будуть ті базиси, в яких має канонічний вигляд, так як їх матриця Грама одинична.

По теоремі 28.6 для квадратичної форми К існує ортонормований базис, в якому вона має діагональний вигляд. Це і є шуканий базис ►.

Зауваження 28.15. Для того, щоб практично привести дві квадратичні форми до діагонального вигляду, Спочатку будують базис, в якому має канонічний вигляд і знаходять матрицю форми К в цьому базисі. Потім шукають власні вектори лінійного оператора, означеного цією матрицею, ортогоналізують їх і нормують, обчислюючи скалярний добуток, вважаючи, що Г = Е. Ортонормований базис з власних векторів – шуканий.

Зауваження 28.16. Якщо ‹_n евклідів простір, то існуючий в ньому скалярний добуток залишають без уваги, а вводять новий скалярний добуток за допомогою квадратичної форми .

Базис, в якому квадратичні форми мають діагональний вигляд, взагалі кажучи, не буде ортонормованим по відношенню до старого скалярного добутку.

[1] ‹‹ - прямий або зовнішній добуток простору ‹ на ‹. Це означає, що елементи цієї множини - впорядковані пари векторів з ‹.

Дата добавления: 2014-01-07