Теорема 28.4. (Закон інерції квадратичної форми)

Кількість коефіцієнтів в канонічному вигляді квадратичної форми, які дорівнюють +1, -1, 0, відповідно, не залежить від способу приведення цієї квадратичної форми до канонічного вигляду.

◄ Нехай на ‹_n квадратична форма рангу r 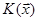має канонічний вигляд в базисі :

Треба довести, що p=q.

Нехай p>q. Переконаємось, що в цьому випадку існує вектор , такий що

(28.9)

В деякому третьому базисі співвідношення (28.9) можна розглядати як систему лінійних однорідних рівнянь відносно 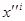шуканого вектора . Так як p>q, то число однорідних рівнянь в (28.9) менше за r, і тому система (28.9) має не нульовий розв’язок відносно 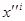. Таким чином, якщо p>q, то існує ненульовий вектор , для якого виконуються співвідношення (28.9). Але

що можливо тільки у випадку, коли

. Останнє означає, що і, відповідно, 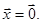Припущення, що p>q веде до протиріччя. Аналогічно перевіряється, що і припущення p<q веде до протиріччя. Тому p=q ►

Означення 28.13. Кількість коефіцієнтів в канонічному вигляді квадратичної форми, які дорівнюють +1, називається додатнім індексом інерції квадратичної форми.

Означення 28.14. Кількість коефіцієнтів в канонічному вигляді квадратичної форми, які дорівнюють –1, називається від’ємним індексом інерції квадратичної форми.

Означення 28.15. Різниця додатного і від’ємного індексів інерції називається сігнатурою квадратичної форми.

Виходячи з попередніх міркувань, очевидними стають наступні твердження (які ми доводити тут не будемо).

Твердження 28.3. Для того, щоб квадратична форма 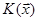, задана на ‹_n була дoдатньо визначена, необхідно і достатньо, щоб додатній індекс інерції дорівнював n.

Твердження 28.4. Для того, щоб квадратична форма 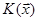, задана на ‹_n, була від’ємна визначена необхідно і достатньо, щоб від’ємний індекс інерції дорівнював n.

Твердження 28.5. Для того, щоб квадратична форма 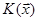, задана на ‹_n була знакозмінною необхідно і достатньо, щоб були відмінні від нуля як додатній, так і від’ємний індекси інерції.

Твердження 28.6. Для того, щоб квадратична форма 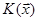, задана на ‹_n, була квазізнакововизначена необхідно і достатньо, щоб або від’ємний індекс інерції дорівнював нулю, а додатній індекс інерції був менший за n, або щоб додатній індекс інерції дорівнював нулю, а від’ємний індекс інерції був менший за n.

Питання про те як з’ясовувати знаковизначеність квадратичних форм не приводячи їх до канонічного вигляду, будуть розглянуті нижче.

Дата добавления: 2014-01-07