Линейные свойства проекций

B b

Свойства линейных операций.

1. Переместительное свойство сложения (коммутативность).

a + b = b + a. {рис.6}

2. Сочетательное свойство сложения (ассоциативность).

(a + b) + c = a + (b + c). {рис.7}

3. Дистрибутивность умножения

а) (λ+μ) а = λ а + μ а. {Очевидно}

б) λ(a+b) = λ a + λ b. {Следует из подобия (рис.8)}

4. λ(μ а) = (λμ) а. {Очевидно }

c

a+b = b+a b+c λ b λ(a+b)

a+bb

a (a+b)+c= a +(b+c) a+b

aa λ a

рис.6 рис.7 рис.8

§3. Проекция вектора на ось.

Определение 1. Осью называется прямая, на которой задано положительное направление.

Числовой осью называют ось, на которой заданы начало отсчета и масштаб (единичный отрезок).

Все точки числовой оси находятся во взаимно – однозначном соответствии с множеством действительных чисел. Началу отсчета, естественно, ставится в соответствие число 0.

Соответствующие точкам числа являются координатами точек относительно этой числовой оси.

Рассматривая некоторую ось u (не числовую), будем предполагать (по умолчанию) наличие единого масштаба во всем пространстве, содержащем эту ось.

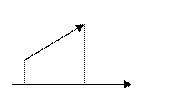Определение 2. Величиной отрезка [ АВ ] (обозначается АВ) называется число, равное длине этого отрезка и взятое со знаком «+», если направлен по оси и со знаком «−», если − против, т.е. .

А' В' и

рис.9

Основные свойства величин отрезков (будем считать, что тт. А, В и С лежат на оси и):

1. АВ = − ВА {Очевидно}
2. 

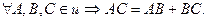
{При расположении точек в указанном порядке по направлению оси − равенство очевидно.

Пусть точки расположены иначе, например: В, С, А → ВА = ВС + СА →

− АВ = ВС − АС → АС = АВ + ВС. Остальные случаи доказываются аналогично}

1. Пусть и – числовая ось, а А_и и В_и − координаты точек А и В на этой оси. Тогда

АВ = В_и − А_и. {Очевидно}

Рассмотрим теперь произвольный вектор и ось u (рис.9).

Определение 3. Ортогональной проекцией вектора на ось и называется величина отрезка А'В', где А' и В' − ортогональные проекции точек А и В на эту ось (рис.9).

Пр _и = А'В'.

Из определения сразу следует, что проекция вектора на ось есть число.

Если начало вектора поместить на ось и угол между вектором и осью обозначить через φ, то для вычисления проекции имеем очевидное соотношение: Пр _и = 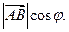При этом необходимо учитывать, что угол φ отсчитывается от оси в положительном направлении, т.е. против часовой стрелки. Если е _и − орт, сонаправленный оси и, то в частном случае .

Замечание. Можно рассматривать и не ортогональные проекции вектора на ось. Для этого следует провести из концов вектора параллельные прямые, не перпендикулярные оси до пересечения с ней. Все основные свойства ортогональных проекций будут выполняться. Однако, в дальнейшем, по умолчанию, все проекции мы будем считать ортогональными.

I. Проекция произведения вектора на число равна произведению числа на проекцию этого вектора: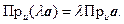

{Доказательство следует из подобия. Необходимо рассмотреть 2 случая: λ > 0 и λ < 0}

II. Проекция суммы векторов сумме проекций этих векторов:

{Для доказательства следует использовать св.2 величин отрезков}

Определение 3. Линейной комбинацией векторов а ₁,…, а _п называется сумма следующего вида:, где все 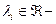коэффициенты линейной комбинации.

(В общем случае, а _i − элементы некоторого множества, которые можно складывать и умножать на действительные числа)

Используя понятие линейной комбинации, можно оба линейных свойства проекций записать одной формулой: 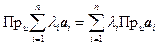: проекция линейной комбинации векторов равна линейной комбинации проекций.

§4. Линейно зависимые и линейно независимые системы векторов.

Определение 1. Система векторов { a ₁ ,…, a _n } называется линейно зависимой, если найдутся коэффициенты λ ₁ ,…,λ_n не все равные нулю, линейная комбинация с которыми равна нулю, т.е.

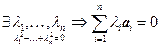
Определение 2. Система векторов { a ₁ ,…, a _n } называется линейно независимой, если ее линейная

комбинация равна нулю только с нулевыми коэффициентами: .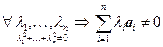

Имеют место несколько простых утверждений.

Теорема 1 (необходимое и достаточное условие линейной зависимости). Векторы а ₁ ,…, a _n – линейно зависимы 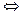когда хотя бы один из них является линейной комбинацией остальных.

{1.(необходимость: { a _k } – л.з.): 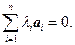Пусть, для определенности,

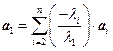, т.е. а ₁ − линейная комбинация остальных.

2.(достаточность: a _m – л.к.): система лин. зав.}

Теорема 2. Если один из векторов системы равен нулю, то вся система линейно зависима.

{0 a ₁ + … + 0 a _{n- 1} +}

Теорема 3. Если подсистема линейно зависима, то и вся система линейно зависима.

{}

Дата добавления: 2014-01-07