Примеры. Отсюда следует, что три вектора на плоскости всегда линейно зависимы

1) 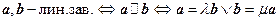. 2) 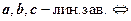они компланарны.

Отсюда следует, что три вектора на плоскости всегда линейно зависимы.

3) Четыре вектора в пространстве всегда линейно зависимы.

4) { f ₁ = 1, f ₂ = x, f ₃ = x ² } – линейно независимы.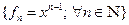

5) {sin² x, cos² x, 1} − линейно зависимы.

§5. Базис. Координаты. Размерность.

Определение 1. Базисом векторного пространства L называется система элементов,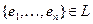

удовлетворяющая двум условиям:

1) система { e ₁,…, e _n } линейно независима.

2) Любой вектор L линейно выражается через базисные (т.е. является линейной комбинацией элементов е ₁, е ₂, …, е _n): .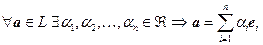

Примеры. Базис на плоскости (V ₂ – 2 неколлинеарных вектора), в пространстве (V ₃ – 3 некомпланарных вектора), в пространстве многочленов степени ≤ n: (1 ,х,х ² ,…,хⁿ).

Теорема 1. Коэффициенты разложения по базису – единственны.

{Пусть }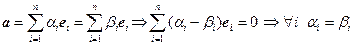

Определение 2. Координатами вектора в некотором базисе называются коэффициенты разложения по этому базису: а = (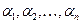) или .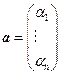

Замечания. 1. В силу Т. 1 данное определение – корректно.

2. В качестве стандарта можно рассматривать как векторы – строки, так и векторы – столбцы.

3. Координаты базисных векторов е ₁, е ₂, е ₃ (в пространстве) в собственном базисе равны:

е ₁ = (1,0,0), е ₂ = (0,1,0), е ₃ = (0,0,1).

Определение 3. Размерностью векторного пространства L (обозначается dim L) называется максимальное число линейно независимых векторов этого пространства.

Если такого числа не существует – пространство называется бесконечномерным.

Теорема 2. Размерность линейного пространства равна числу базисных векторов. {б/д}

Отсюда, в частности, следует, что все базисы одного пространства состоят из одинакового числа векторов.

Примеры. V ₂; V ₃; Rⁿ; C[ a, b ].

Результаты линейных операций легко вычисляются в координатной форме.

Теорема 3. При сложении векторов их соответствующие координаты складываются:

.

{}

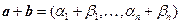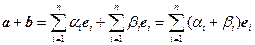Теорема 4. При умножении вектора на число его координаты умножаются на это число:

λ а = (λ α ₁ ,…,λ α _n). {д – во аналогично}

В заключение рассмотрим пример базиса, который используется наиболее часто.

Определение 4. Ортонормированным базисом в пространстве называется базис, состоящий из трех взаимно ортогональных векторов единичной длины (на плоскости – из двух).

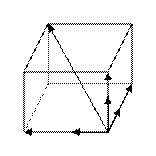
Эти векторы обозначают буквами i, j и k и называют

базисными ортами. Таким образом, выполняются соотношения

Дата добавления: 2014-01-07