Принцип Даламбера

Цель лекции - изложить принцип Даламбера для материальной точки и механической системы

План лекции

3.1 Принцип Даламбера для материальной точки;

3.2 Принцип Даламбера для механической системы.

3.1 Принцип Даламбера сформулирован в 1743 году и первоначально, в отличие от законов Ньютона, был предназначен для изучения движения несвободных механических систем. В настоящее время этот принцип и вытекающий из него метод кинетостатики рассматривают как удобный прием для определения реакций связей и сил взаимодействия, а также для составления дифференциальных уравнений движения механических систем. В соответствии с аксиомами динамики основное уравнение движения материальной точки имеет вид:

, (6.4)

где - равнодействующая активных сил; - равнодействующая реакций связей; - абсолютное ускорение точки.

Уравнение (6.4) можно также записать в виде

Слагаемое (- та) обозначают и называют Даламберовой силой инерции (или просто силой инерции). Основное уравнение динамики материальной' точки при использовании силы инерции принимает следующий вид:

(6.5)

Так как „указанные выше силы образуют систему сходящихся сил, то уравнение (6.5) можно рассматривать как условие равновесия системы сил (). В этом и состоит принцип Даламбера для материальной точки: при движении материальной точки в любой момент времени приложенные к ней активные силы и реакции связей вместе с силой инерции образуют систему сил, эквивалентную нулю, т.е.

~0 (6.6)

В проекциях на оси декартовой системы координат имеем

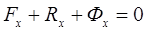
(6.7)

где ; ; ; в проекциях на оси естественного трехгранника получаем:

(6.8)

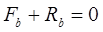
где ;

Предоставление основного уравнения динамики материальной точки в виде (6.5) слёдует рассматривать как прием, удобный для решения задач, например для определения сил взаимодействия и реакций связей.

Контрольные задания для СРС – рассмотреть и решить следующую задачу самостоятельно: груз массой т движется по наклонной плоскости с углом наклона ; коэффициент трения груза о плоскость равен . Одинаковы ли дифференциальные уравнения движения груза по этой плоскости йниз и вверх? [1-4] Рассмотреть сложное движение точки с применением понятия силы инерции [1-4]

Тема 7. Общие теоремы динамики точки – 2 часа

Цель лекции – познакомить с мерой действия силы – работой и мощностью; рассмотреть некоторые примеры вычисления работы некоторых сил

План лекции:

1. Элементарная и полная работа силы. Пример. Мощность силы.

2. Работа силы в различных случаях движения твердого тела.

3. Кинетическая энергия материальной точки и механической системы. Вычисление кинетической энергии при различных движениях твердого тела

4. Теоремы об изменении кинетической энергии материальной точки и механической системы. Закон сохранения механической энергии

Краткое содержание лекции

Элементарная работа силы. Элементарная работа силы на элементарном перемещении определяется формулой

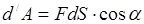, (7.1)

где , 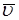- скорость точки приложения силы

Величина 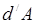скалярная, ее знак определяется знаком функции . Если острый угол, - тупой угол, а для , . Так как , то формулу (1) можно представить в виде:

. (7.2)

Таким образом, элементарная работа силы равна произведению элементарного переемещения на проекцию силы на это перемещение

Поскольку , то, согласно (1)

, или

(7.3)

Следовательно, элементарная работа силы равна скалярному произведению вектора силы и дифференциала радиус-вектора .

Так как, 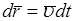представим выражение (7.3) в виде

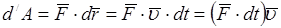(7.4)

Таким образом, элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки ее приложения.

В аналитической форме (7.4) будет иметь вид:

(7.5)

Полная работа силы. Полную работу силы на конечном перемещении определяют как предел суммы ее элементарных работ, т.е.

(5)

где работа силы на элементарном перемещении.Так как эта сумма является интегральной суммой определения криволинейного интеграла, то

.

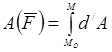Используя различные формулы для определения элементарной работы, получаем:

или

.

Если же сила является функцией времени, то, согласно (7.4), работа силы определяется выражением:

(7.6)

Работа силы зависит от характера движения точки приложения силы. Например, если скорость точки приложения силы равна нулю, то .

Мощность. Отношение приращения работы силы к элементарному промежутку времени, за которое оно произошло, называется мощностью:

. (7.7)

Так как 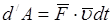, то ..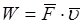

Таким образом, мощность силы равна скалярному произведению силы на скорость точки ее приложения. Единица измерения мощности в системе СИ 1 Ватт .

Работа силы при поступательном движении твердого тела. При поступательном движении твердого тела векторы скоростей, а также элементарные перемещения всех точек тела одинаковы. Тогда элементарная работа силы

. (7.8)

Полная работа силы на каком-либо перемещении будет

Кинетическая энергия материальной точки и системы. Кинетическую энергию материальной точки определяют по формуле:

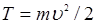, (7.9)

где есть скорость точки.

Кинетическая энергия механической системы равна сумме кинетических энергий всех точек системы:

(7.10)

Кинетическая энергия – положительная скалярная величина. Единицей измерения кинетической энергии в системе СИ является – джоуль (1Дж=1Н∙м).

Кинетическая энергия твердого тела. При поступательном движении твердого тела скорости всех точек одинаковы и равны скорости центра масс, поэтому кинетическая энергия

, (7.11)

где- масса твердого тела.

При вращении твердого тела вокруг неподвижной оси скорость его произвольной точки

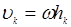. (7.12)

Тогда

, (7.13)

где - момент инерции тела относительно оси вращения.

При плоском движении твердого тела, которое можно рассматривать как совокупность поступательного движения вместе с центром масс С и вращения вокруг подвижной оси CZ с угловой скоростью , кинетическая энергия тела будет определяться формулой:

, (7.14) где момент инерции тела относительно оси OZ.

Теорема об изменении кинетичской энергии материальной точски.

. (7.15)

Эта формула выражает теорему об изменении кинетической энергии точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.

Разделив обе части уравнения на , получим еще одну запись теоремы в дифференциальной форме:

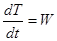. (7.16)

После интегрирования получим

(7.17)

где - кинетическая энергия точки в начальный и конечный моменты времени соответственно.

Эта формула выражает теорему об изменении кинетической энергии в интегральной форме: изменение кинетической энергии точки на любом перемещении равно работе силы, действующей на точку, на том же перемещении.

Теорема об изменении кинетической энергии механической системы. Для механической системы, на которую действуют как внешние, так и внутренние силы, можно записать:

. (7.18)

Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.

Разделив обе части уравнения на . Тогда

. (7.19)

Таким образом, первая производная по времени от кинетической энергии системы равна сумме мощностей всех внешних и внутренних сил, действующих на точки системы

Проинтегрировав дифференциальные уравнения, будем иметь

, (7.20)

где - кинетическая энергия системы в начальном и текущем положениях соответственно; ,соответственно работа внешней и внутренней силы, действующей на k- ю точку системы.

Таким образом: изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек приложения этих сил.

Рекомендуемая литература: [1-4; 7] [10-12; 16, 17]

Контрольные задания для СРС – 1) Влияют ли внутренние силы системы на изменение ее кинетической энергии? 2) В каких механических системах сумма работ внутренних сил равна нулю?

Тема 8. Техническая механика. Гипотезы и принципы сопротивления материалов – 2 часа.

Дата добавления: 2014-01-07