Моменты инерции

Моменты инерции сечения определяются так (рисунок 1):

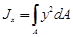
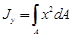
. (4.4)

называются осевыми моментами инерции,

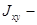центробежным моментом.

Если исходные оси центральные, то при параллельном переносе осей (рисунок 4.1) моменты инерции изменяются на величину, равную произведению площади на квадрат расстояния между осями

(4.5)

Оси, относительно которых центробежный момент равен нулю, называются главными осями. Главные оси всегда проходят через центр тяжести, (являются центральными) и положение их определяется по формуле

. (4.6)

Здесь угол наклона главных осей к исходным осям . Если сечение имеет ось симметрии, то главная ось совпадает с ней, а вторая главная ось проходит перпендикулярно ей через центр тяжести.

Моменты инерции относительно главных осей называются главными моментами. Относительно главных осей осевые моменты экстремальны (), а центробежный момент равен нулю ().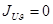

Главные моменты определяются по формуле

. (4.7)

Главные моменты простейших фигур.

Прямоугольник:

,

где 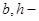стороны параллельные осям соответственно.

Круг:

Главные моменты стандартных принятых профилей даются в таблицах ГОСТа.

Рекомендуемая литература:

[13], [18] Контрольные задания для СРС – изучить самостоятельно тему: «Геометрические характеристики»

Тема 5. Введение в раздел «Кинематика». Кинематика точки – 2 часа.

План лекции:

1. Основная задача кинематики. Кинематика точки.

2. Способы задания движения точки.

Краткое содержание лекции

1. Кинематика делится на кинематику точки и кинематику твердого тела. В кинематике время t принимается за независимое переменное, а все другие кинемати­ческие характеристики (расстояние, скорость, ускорение и т.п.) рассматриваются как функции времени.

Основной задачей кинематики является определение всех кинематических величин, характеризующих движение, как отдельной точки, так и тела в целом. Эта задача может быть решена путем применения различных способов кинематического задания движения точки.

2. Векторный способ задания движения точки. Движение точки можно задать, если выразить ее радиус-вектор в некоторой системе отсчета в виде функции времени

(5.1)

Функция для определенности дальнейших рассуждений предполагается непрерывной, дважды дифференцируемой. Такое задание радиус-вектора точки предполагает наличие системы отсчета, но не конкретизирует ее. В данном случае траекторию точки можно определить как годограф ее радиус-вектора, т.е. геометрическое место концов радиус-вектора , изменяющегося во времени.

Скорость точки при векторном способе задания движения есть векторная величина, равная первой производной по времени от радиус-вектора точки; скорость всегда направлена по касательной к траектории в сторону движения точки, а ее численное значение определяется модулем .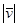

Единица измерения скорости в СИ – м/с.

(5.2)

Ускорение точки по своему физическому смыслу есть изменение скорости, и определяется как первая производная по времени от скорости точки или как вторая производная от радиус – вектора точки. численное значение ускорения определяется модулем .

(5.3)

Единица измерения ускорения в СИ - м/с².

Координатный способ задания движения точки. Чтобы знать положение точки в пространстве в любой момент времени необходимо иметь уравнения движения точки в виде

x=x(t), y=y(t), z=z(t) (5.4)

Эти выражения представляют собой уравнения движения точки в декартовой системе координат и одновременно являются уравнениями траектории точки, записанными в параметрической форме.

Чтобы найти уравнение траектории в форме непосредственной зависимости между координатами x, y, z, из уравнений движения необходимо исключить время

В рассматриваемом случае скорость точки представляет собой сумму следующих векторов, параллельных осям декартовой системе координат:

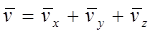(5.5)

а ее численное значение (модуль) определится по формуле

(5.6)

Формула для расчета ускорения примет вид

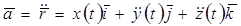, (5.7)

а численное значение ускорения будет равно модулю вектора :

. (5.8)

Естественный способ задания движения точки. Если траектория точки известна, то знаки можно естественным способом. Для этого необходимо: зафиксировать на траектории точку начала отсчета, выбрать положительное и отрицательное направления движения и указать закон движения точки по траектории в виде

. (5.9)

Всего этого в совокупности достаточно для однозначного определения положения точки в пространстве в любой момент времени.

Согласно основному определению скорости и с учетом определения единичного вектора ,

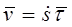. (5.10)

Отсюда следует, что проекция скорости точки на ось, касательную к траектории точки, равна

. (5.11)

Эту производную иногда называют алгебраической скоростью. Для ускорения имеем

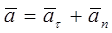(5.12)

Проекции ускорения на оси естественной системы координат (касательную, нормаль и бинормаль) равны: ; .

Очевидно, что 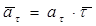, , 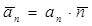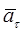^, и модуль ускорения

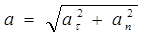. (5.13)

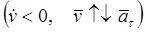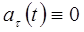Характер движения точки по траектории можно определить, исходя из знака произведения скорости и ускорения: в случае - движение точки ускоренное, ; в случае - движение точки замедленное . При движение точки равномерное , в этом случае при движении по криволинейной траектории , и ^.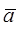

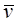Контрольные задания для СРС – рассмотреть самостоятельно естественный трехгранник (оси естественной системы координат).

Тема 3. Введение в раздел «Динамика». Принцип Даламбера – 2 часа

План лекции:

1. Предмет динамики. Основные законы динамики.

2. Дифференциальные уравнения движения материальной точки. Две задачи динамики.

3. Принцип Даламбера.

Краткое содержание лекции

1. Динамика является основным и наиболее общим разделом теоретической механики. В динамике изучают зависимость между движением материальных объектов и действующими на них силами.

Соотношения между основными понятиями динамики определяются аксиомами или основными законами движения, данными Ньютоном.

1 закон. Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

2 закон (основной). Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и совпадает с ней по направлению.

Математически этот закон можно записать в виде I

(6.1)

где - ускорение точки, т - характеризует инертные свойства точки и называется массой.

3 закон (действия и противодействия). Действию всегда есть равное и противоположное противодействие, иначе взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Если на материальную точку действует система сил , то действие каждой из сил не зависит от действия остальных и каждая из сил сообщает точке такое ускорение, какое она ей сообщила бы, если бы действовала одна, а под действием системы сил точка получает ускорение

где . в этом заключается принцип независимости действия сил.

2. Так как ускорение точки связано с ее радиус-вектором , а сила в рамках классической механики может быть функцией времени, положения и скорости точки, из уравнения (6.1) получаем векторное дифференциальное уравнение движения точки:

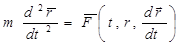. (6.2)

В проекциях на декартовы оси (базис ) дифференциальные уравнения движения точки имеют вид

;

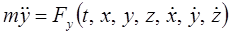; (6.3)

;

Здесь - проекции ускорения точки на координатные оси, проекции равнодействующей сил, действующих на точку.

На основе дифференциальных уравнений движения материальной точки решают две задачи динамики точки: 1) по движению определить силы, производящие данное движение. Эту задачу называют прямой задачей динамики. 2) - даны силы, действующие на данный материальный объект; требуется определить движение этого объекта под действием данных сил. Эту задачу называют второй задачей динамики.

Дата добавления: 2014-01-07