
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение. Правила и формулы дифференцирования
|
|
|
|
Пусть на плоскости с д.п.с.к. X0Y определена функция y=f(x) в некоторой т.  .
.
| Def.1 | (Наизусть!) Производной функции y=f(x) в т. x называют пределотношения приращения функции к приращению аргумента, когда последнее стремится к нулю, т.е.
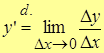 ,
где ,
где 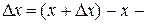 приращение аргумента; приращение аргумента;
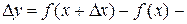 приращение функции. приращение функции.
|
| Note | Приращение аргумента 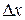 может быть как больше нуля, так и меньше нуля. может быть как больше нуля, так и меньше нуля.
|
| Def.2 | Функция y=f(x) называется дифференцируемой в т. х, если в этой точке существует конечная производная. |
Обозначение производной
y' или f '(x) – по Лагранжу;
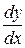 или
или 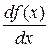 – по Лейбницу;
– по Лейбницу;
Dy или Df(x) – по Коши;
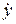 или
или 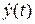 – по Ньютону.
– по Ньютону.
В данном курсе мы будем применять первые два типа обозначений (т.е. по Лагранжу или по Лейбницу), обозначение по Ньютону применяют в курсе «Теоретическая механика».
Основные правила и формулы дифференцирования
Правила
Пусть функции y=f(x), u=u(x), v=v(x) – определены и дифференцируемы в т.  .
.
Пусть с – произвольная постоянная (с – const).
Пусть y=y[u(x)] – сложная функция от основного аргумента x (u(x) – называют промежуточным аргументом).
Тогда:
1. 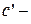 производная константы;
производная константы;
2. 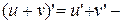 производная суммы функций;
производная суммы функций;
3. 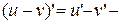 производная разности функций;
производная разности функций;
4. 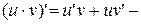 производная произведения функций;
производная произведения функций;
5. 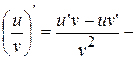 производная частного функций;
производная частного функций;
6.  производная обратной функции;
производная обратной функции;
7. 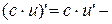 где с – const;
где с – const;
8. 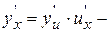 производная сложной функции.
производная сложной функции.
При выводе данных правил полагаем, что
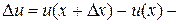 приращение функции u;
приращение функции u;
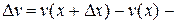 приращение функции v.
приращение функции v.
Формулы
Таблица производных элементарных функций
1. 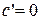
2. 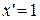
3. 
4. 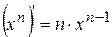
5. 
6. 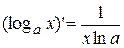
7. 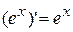
8. 
9. 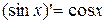
10. 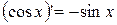
11. 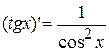
12. 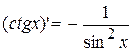
13. 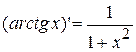
14. 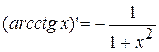
15. 
16. 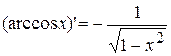
| Т. | (Связь между дифференцируемостью и непрерывностью функции) Если функция y=f(x) дифференцируема в т. x, то она непрерывна в т. х (обратное не всегда верно!). |
Proof:
1-й метод. Пусть  , тогда по лемме переменная
, тогда по лемме переменная 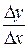 отличается от предела
отличается от предела  на б.м.в. α, т.е.
на б.м.в. α, т.е. 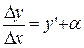 . Откуда
. Откуда 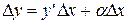 . Пусть
. Пусть 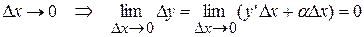 , ч.т.д.
, ч.т.д.
2-й метод. Пусть  .
.
Тогда  , ч.т.д.
, ч.т.д.
Мы воспользовались одним из определений непрерывности функции y=f(x)
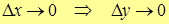 .
.
Правила
Proof:
1. 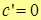 , т.е. производная константы равна нулю.
, т.е. производная константы равна нулю.
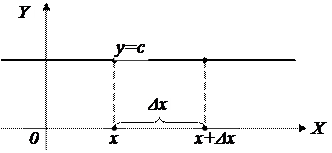 Proof:
Proof:
 , ч.т.д.
, ч.т.д.
2.  , т.е. производная суммы функций.
, т.е. производная суммы функций.
Proof:
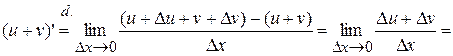
 , ч.т.д.
, ч.т.д.
3. 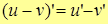 , т.е. производная разности функций.
, т.е. производная разности функций.
Proof:

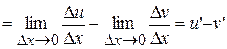 , ч.т.д.
, ч.т.д.
4.  , т.е. производная произведения функций.
, т.е. производная произведения функций.
Proof:
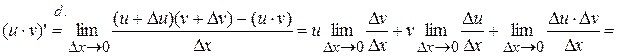
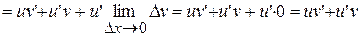 , ч.т.д.
, ч.т.д.
5. 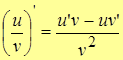 , т.е. производная частного функций.
, т.е. производная частного функций.
Proof:
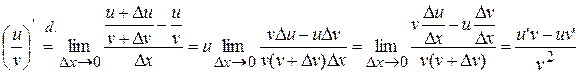 , ч.т.д.
, ч.т.д.
6. 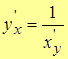 , т.е. производная обратной функции.
, т.е. производная обратной функции.
Proof:
 , ч.т.д.
, ч.т.д.
7. 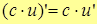 , где с – const.
, где с – const.
Proof:
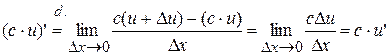 , ч.т.д.
, ч.т.д.
8. 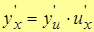 , т.е. производная сложной функции.
, т.е. производная сложной функции.
Proof:
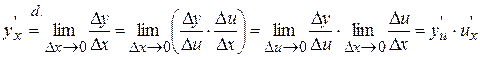 , ч.т.д.
, ч.т.д.
Формулы
Proof:
| Note | Приведем вывод некоторых формул, при этом нарушив их порядок. Остальные формулы вывести дома или на п/з. |
5. 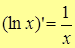 .
.
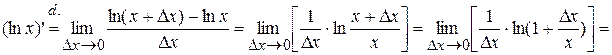

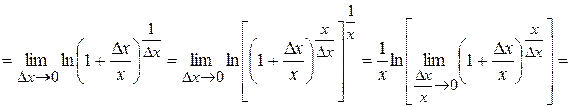
 , ч.т.д.
, ч.т.д.
6. 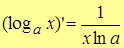 .
.
 , ч.т.д.
, ч.т.д.
7. 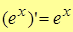 .
.
Пусть ex =y, тогда x= ln y или 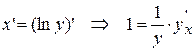 , (т.к. y – сложная функция переменной х). Или
, (т.к. y – сложная функция переменной х). Или 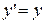 , т.е.
, т.е. 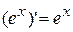 , ч.т.д.
, ч.т.д.
8.  .
.
Пусть 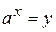 , тогда
, тогда 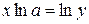 , или
, или 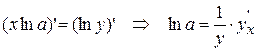 (т.к. y – сложная функция переменной х). Или
(т.к. y – сложная функция переменной х). Или  , т.е.
, т.е.  , ч.т.д.
, ч.т.д.
4. 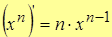 .
.
Пусть 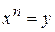 , тогда
, тогда 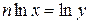 или
или 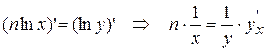 (т.к. y – сложная функция переменной x).
(т.к. y – сложная функция переменной x).
Или  , т.е.
, т.е.  ,
, 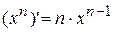 , ч.т.д.
, ч.т.д.
9. 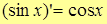 .
.
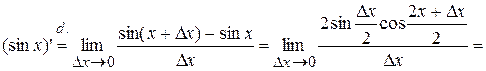
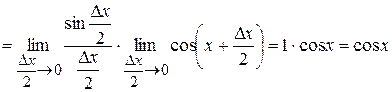 , ч.т.д.
, ч.т.д.

10. 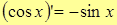 .
.
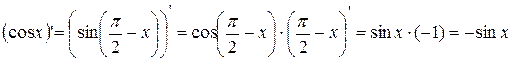 , ч.т.д.
, ч.т.д.
15. 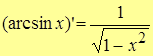 .
.
Пусть 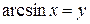 , тогда
, тогда 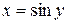 , или, учитывая, что
, или, учитывая, что 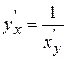 , т.е.
, т.е.
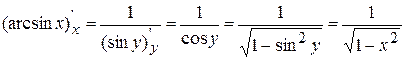 , т.е.
, т.е.  , ч.т.д.
, ч.т.д.
| Note | Т.к. 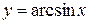 монотонно возрастает на монотонно возрастает на 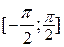 , то в последней формуле перед радикалом выбираем знак «+». , то в последней формуле перед радикалом выбираем знак «+».
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 326; Нарушение авторских прав?; Мы поможем в написании вашей работы!