
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрический смысл производной и дифференциала
|
|
|
|
Дифференциал. Инвариантность формы записи дифференциала
Пусть функция y=f(x) определена и дифференцируема в т.  , т.е.
, т.е.  , это значит, что переменная
, это значит, что переменная 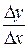 отличается от предела y’ на б.м.в. (при
отличается от предела y’ на б.м.в. (при 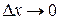 ).
).
Т.е. 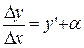 или
или 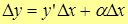 – приращение функции.
– приращение функции.
Если  .
.
Произведение двух б.м.в. есть б.м.в. более высокого порядка малости, чем 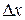 , т.е.
, т.е.  .
.
Т.о. 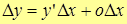 .
.
Более того, б.м.в. 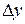 и
и 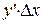 эквиваленты, т.е. предел их отношения равен единице, т.е.
эквиваленты, т.е. предел их отношения равен единице, т.е.
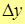 ~
~ 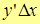 .
.
| Note 1 | В приближенных методах вычисления используется запись
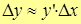 . .
|
| Т. | Если две б.м.в. эквиваленты, то каждая из них является главной частью другой.
Т.е. если α ~ β (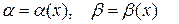 при при 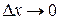 ), то ), то
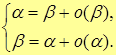
|
Proof:
Пусть α ~ β  , тогда по лемме переменная
, тогда по лемме переменная  отличается от предела 1 на б.м.в., т.е.
отличается от предела 1 на б.м.в., т.е.
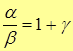 , где γ – б.м.в. (если
, где γ – б.м.в. (если 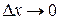 ).
).
Откуда 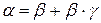 , но
, но 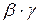 - б.м.в. более высокого порядка малости, чем
- б.м.в. более высокого порядка малости, чем  , т.е.
, т.е.  , ч.т.д.
, ч.т.д.
| Note 2 | Дома или на п/з аналогично доказать, что
 . .
|
| Def. | (Наизусть!) Дифференциалом функции y=f(x) в т.  называют главную, линейную относительно приращения аргумента часть приращения функции, т.е. если называют главную, линейную относительно приращения аргумента часть приращения функции, т.е. если
 ,
то ,
то  – дифференциал функции. – дифференциал функции.
|
| Note 3 | В математике принято приращение аргумента считать дифференциалом аргумента, т.е.  , тогда , тогда
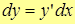 .
Откуда .
Откуда  – читается «дэ игрек по дэ икс». – читается «дэ игрек по дэ икс».
|
| Note 4 | Следовательно, если 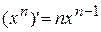 , то , то  ;
если ;
если  , то , то  и т.д. и т.д.
|
| Note 5 | Дома или на п/з составить таблицу дифференциалов элементарных функций. |
Инвариантность формы записи дифференциала
1. Пусть x – основной аргумент функции y=f(x),  .
.
Тогда дифференциал  .
.
2. Пусть x – промежуточный аргумент сложной функции y=y[x(t)].
Тогда по определению дифференциала  , или, учитывая формулу дифференцирования сложной функции
, или, учитывая формулу дифференцирования сложной функции  , получим
, получим
 ,
,
т.е. формула записи для дифференциала не изменилась. Это свойство дифференциала называют инвариантностью:
 .
.
Пусть на плоскости с д.п.с.к. X0Y определена и дифференцируема функция y=f(x) в некоторой области т.  .
.
1. Тогда приращение функции  .
.
2. Приращение касательной  .
.
Действительно, пусть две точки M и N принадлежат кривой L.
| Def.1 | Секущей называют прямую, проходящую через любые две точки кривой. |
| Def.2 | Касательной к кривой L в т. M называют предельное положение секущей при N→M. |
 |
Пусть кривая L в д.п.с.к. X0Y задана явно y=f(x).
Тогда из прямоугольного  , если т. N → т. M, то
, если т. N → т. M, то 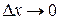 , или угловой коэффициент касательной
, или угловой коэффициент касательной
 .
.
Пусть т. M0 (x0, y0) 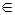 L, тогда уравнение прямой, проходящей через т. М0 с заданным угловым коэффициентом k, имеет вид
L, тогда уравнение прямой, проходящей через т. М0 с заданным угловым коэффициентом k, имеет вид
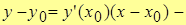 уравнение касательной.
уравнение касательной.
Пусть нормаль – прямая, проходящая через т. М0 перпендикулярно касательной, тогда
 уравнение нормали.
уравнение нормали.
| Note! | Дифференциал геометрически равен приращению касательной, в отличие от приращения функции. |
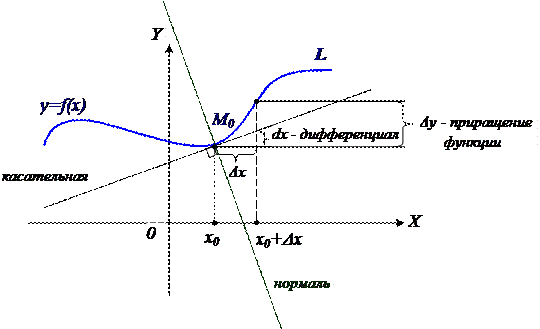
| Note! | Следует заметить, что (в зависимости от выпуклости или вогнутости графика функции y=f(x)) дифференциал dy может быть как меньше, так и больше приращения функции. Однако в любом случае дифференциал – главная, линейная его часть. |
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 756; Нарушение авторских прав?; Мы поможем в написании вашей работы!