
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производные и дифференциалы высших порядков
|
|
|
|
Приложение дифференциала к приближенным вычислениям
Т.к. приращение функции 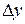 и дифференциал dy – эквивалентные б.м.в. (при
и дифференциал dy – эквивалентные б.м.в. (при 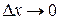 ), т.е.
), т.е.
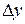 ~
~ 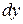 ,
,
то в приближенных методах вычислений пишут
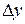 ≈
≈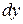 ,
,
с точностью до б.м.в. более высокого порядка малости.
Учитывая, что дифференциал функции по определению
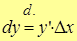 ,
,
получим
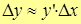 .
.
Или
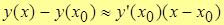 ,
,
откуда
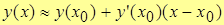 .
.
Ex.1. Применяя дифференциал вычислить приближенно значение функции
y=sinx в т. x=10, т.е. sin 10.
Решение:
Пусть x0 =00, x =10, тогда Δx =10 – 00 = 10.
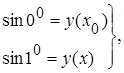 тогда
тогда 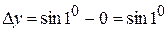 .
.
Т.к. производная 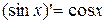 , то
, то 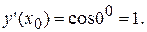
Или
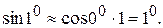
В радианах 10  .
.
Т.о. 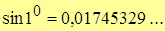 .
.
Заметим, что точное значение
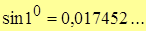 .
.
Т.о., абсолютная погрешность не превышает одной десятитысячной.
Пусть функция y=y(x) определена и дифференцируема в т.  . Тогда
. Тогда 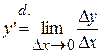 называют производной 1-го порядка. Т.к. производная 1-го порядка также является функцией, то ее можно дифференцировать.
называют производной 1-го порядка. Т.к. производная 1-го порядка также является функцией, то ее можно дифференцировать.
| Def. | Производной 2-го порядка называют производную от производной 1-го порядка, т.е.
 – производная 2-го порядка (по Лагранжу)
или – производная 2-го порядка (по Лагранжу)
или
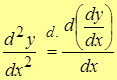 – производная 2-го порядка (по Лейбницу). – производная 2-го порядка (по Лейбницу).
|
Символ 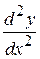 можно рассматривать как единый символ, который читается как «дэ два игрек по дэ икс дважды».
можно рассматривать как единый символ, который читается как «дэ два игрек по дэ икс дважды».
Однако, учитывая, что  , то
, то 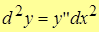 .
.
Т.о., мы получили формулу для вычисления дифференциала 2-го порядка, т.е. 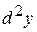 – дифференциал 2-го порядка.
– дифференциал 2-го порядка.
Аналогично вычисляются дифференциалы 3-го порядка 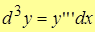 , 4-го порядка
, 4-го порядка  , и т.д.
, и т.д.
Ex.1. Вычислить дифференциал 3-го порядка для функции y=sinx.
Решение.
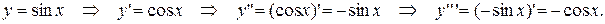
Т.о.,
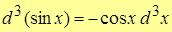 .
.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 319; Нарушение авторских прав?; Мы поможем в написании вашей работы!