
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференцирование неявной функции и функции, заданной параметрически
|
|
|
|
1. Дифференцирование функции, заданной неявно
Пусть функция y=y(x) задана неявно, т.е. F(x;y)= 0 или F(x;y(x))= 0.
Если функция F(x;y) – непрерывно дифференцируема в некоторой области D координатной плоскости X0Y, причем, частная производная функции двух переменных 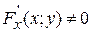 , то можно доказать, что
, то можно доказать, что
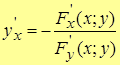 .
.
Эта формула будет доказана далее в разделе «Функции нескольких переменных». Следует заметить, что переменные в функции F(x;y) считаются независимыми.
Однако не обязательно разрешать уравнение F(x;y)= 0 относительно y. Достаточно продифференцировать это уравнение, считая y не переменной, а функцией аргумента x.
Ex. 1. Вычислить производную 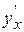 , если уравнение задано неявно
, если уравнение задано неявно 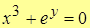 .
.
Решение.
Продифференцируем это уравнение по переменной x, считая y=y(x), тогда получим
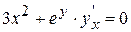 .
.
Откуда 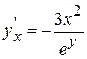 или, учитывая (из заданного уравнения), что
или, учитывая (из заданного уравнения), что 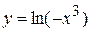 , получим
, получим 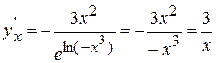 .
.
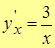 .
.
2. Дифференцирование функции, заданной параметрически
Пусть функция y=y(x) задана параметрически, т.е.
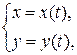 где параметр
где параметр 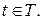
По правилу дифференцирования сложной и обратной функции
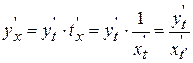 .
.
Т.о.,
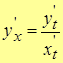 .
.
Ex. 2. Найти производную 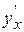 , если функция задана параметрически
, если функция задана параметрически 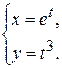
Решение.
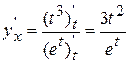 , т.о.,
, т.о., 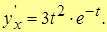
ГЛАВА 7. Теоремы о среднем
8.1. Теорема Ферма [13]
| Т. | (Теорема Ферма) Пусть функция y=f(x) определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда, если в т. 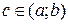 функция достигает локального экстремума, то функция достигает локального экстремума, то 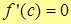 . .
|
| Note 1 | Локальным экстремумом называют локальный («местный») максимум или минимум. |
Proof:
Пусть в т. 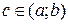 функция y=f(x) достигает локального максимума.
функция y=f(x) достигает локального максимума.
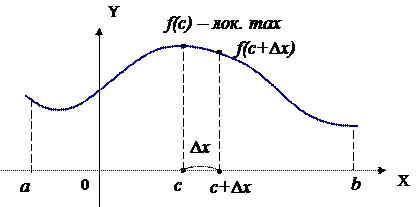 |
По определению производной 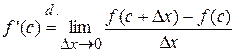 .
.
| Note 2 | Приращение аргумента может быть любым, т.е. 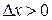 или или 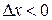 . .
|
1. Пусть 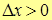
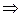
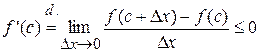 , т.к. числитель имеет знак «-», а знаменатель знак «+».
, т.к. числитель имеет знак «-», а знаменатель знак «+».
2. Пусть 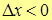
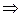
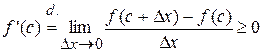 , т.к. числитель имеет знак «-», и знаменатель знак «-».
, т.к. числитель имеет знак «-», и знаменатель знак «-».
| Note 3 | f '(c) – значение производной в т. с. Это значение не может быть одновременно меньше или больше нуля. Т.о. f '(c) =0, ч. т. д. |
8.2. Теорема Ролля [14]
| Т. | (Теорема Ролля) Пусть функция y=f(x) определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда, если на концах отрезка функция принимает равные значения f(a)=f(b), то 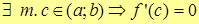 . .
|
Proof:
По второй теореме Вейерштрасса – функция, непрерывная на отрезке, достигает своего максимального М и минимального m значения.
Возможны два варианта:
1. Пусть М=m на [a;b] 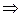 функция
функция 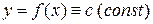 .
.
Тогда в 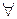 т.
т. 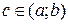
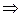
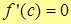 , ч.т.д.
, ч.т.д.
2. Пусть 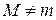 , тогда по теореме Ферма (п.7.1.)
, тогда по теореме Ферма (п.7.1.) 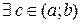
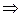
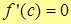 , ч.т.д.
, ч.т.д.
7.3. Теорема Лагранжа [15]. Геометрический смысл
| Т. | (Теорема Лагранжа) Пусть функция y=f(x) определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда, 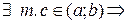 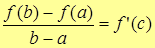 . .
|
Proof:
Чтобы воспользоваться теоремой Роля (п.7.2.) введем вспомогательную функцию
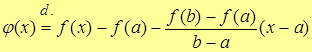 .
.
Очевидно, что 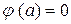 и
и 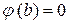 , тогда по теореме Роля
, тогда по теореме Роля 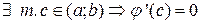 .
.
Но, производная 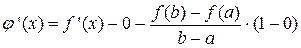 .
.
В т.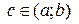 производная
производная 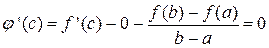 (по теореме Ролля).
(по теореме Ролля).
Или 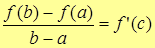 , ч.т.д.
, ч.т.д.
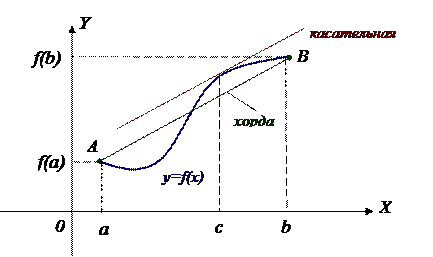
Геометрический смысл
Очевидно, что 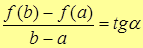 – тангенс угла «наклона» хорды, соединяющей точки
– тангенс угла «наклона» хорды, соединяющей точки 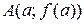 и
и 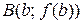 к оси ОХ.
к оси ОХ.
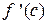 – угловой коэффициент касательной к графику функции в т.
– угловой коэффициент касательной к графику функции в т. 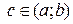 .
.
| Note | Таким образом, тангенс угла «наклона» хорды равен угловому коэффициенту касательной в т. 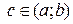 . .
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1364; Нарушение авторских прав?; Мы поможем в написании вашей работы!