Параметры распределения РИ и ПИ

Описание случайных погрешностей с помощью функции распределения наиболее правильно, однако определить функцию 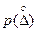в большинстве случаев по экспериментальным данным невозможно, поэтому на практике при нормировании случайных РИ и ПИ принимают значения числовых величин, которые называются начальными и центральными моментами.

В теории вероятности начальными моментами порядка R случайной величины Х определяют по формуле:

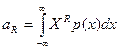. (2.23)

Практическое значение имеет начальный момент I-го порядка, R=1, который называется математическим ожиданием и определяется для непрерывных и дискретных величин по следующим формулам:

– для непрерывных величин

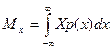; (2.24)

– для дискретных случайных величин

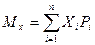, (2.25)

где P_i – вероятность появления конкретного результата наблюдения k_i.

Центральный момент II-го порядка, R=2, называется дисперсией (D_x) случайной величины Х. Определяется по формуле:

– для непрерывной случайной величины Х

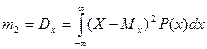, (2.26) где М_х – математическое ожидание, определяется выражением (2.24);

– для дискретных случайных величин

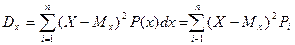, (2.27)

где М_х – математическое ожидание, определяется выражением (2.25).

В выражениях (2.27), (2.26) скобка 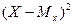представляет собой согласно рис. 2.11. квадрат случайной погрешности единичного измерения:

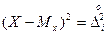. (2.28)

Это позволяет утверждать, что дисперсия

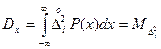(2.29) представляет собой математическое ожидание квадратной случайной погрешности, т.е. характеризует рассеяние результатов конкретных РИ единичных Х_і от математического ожидания М_х, принятого за результат групового измерения.

Размерность дисперсии:

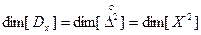. (2.30)

Это неудобно, поскольку принято отклонение величин характеризовать в тех же величинах, что и сами измерения. Исходя из этого, в качестве меры рассеивания случайных РИ Х_i от математического ожидания применяют среднеквадратическое отклонение (СКО) δ_х , определяемые по формуле δ_х=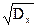. (2.31)

Размерность СКО:

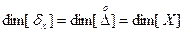. (2.32)

δ_х представляет собой очень важную характеристику случайной ПИ. Она фактически выражается через СКО, что будет показано далее, поэтому задача вычисления СКО δ_х представляет собой третью важную задачу математической обработки задачи после расчёта М_х и поправок , .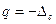

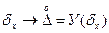Дата добавления: 2014-01-07