Сопряжения

Сопряжением называют плавный переход одной прямой линии или дуги окружности в другую прямую линию или дугу окружности. Центр сопрягающей дуги называется - центром сопряжения. Он определяется в пересечении двух вспомогательных линий параллельных заданным прямым или в пересечении двух дуг концентричным заданным дугам и отстоящих от заданных линий на расстоянии радиуса сопряжения.

Общая для этих линий точка называется точкой сопряжения. Точка сопряжения будет находиться: при сопряжении двух прямых на перпендикуляре, опущенном из центра сопряжения к самим прямым, при сопряжении двух дуг на прямых (или их продолжениях) соединяющих центры данных дуг.

Сопряжения двух прямых, являющихся сторонами прямого (рис.14 а), острого (рис. 14 б) или тупого (рис. 14 в) углов, посредством дуги радиуса R.

а) б) в)

Рисунок 14. Сопряжение угла: а) прямого; б) острого; в) тупого

Во всех этих случаях поступают так:

1. Проводят две вспомогательные прямые линии, параллельные сторонам угла, на расстоянии от этих сторон, равном радиусу дуги R.

2. Находят точку О пересечения этих вспомогательных прямых. Точка О является центром дуги радиуса R, сопрягающей стороны угла т.е.центром сопряжения. Из этого центра О описывают дугу, плавно переходящую в прямые – стороны угла.

3. Дугу заканчивают в точках сопряжения n и n₁, которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла.

Следует отметить, что сопряжения могут быть:

1.Внешние - центры всех сопрягаемых дуг находятся по разные стороны от точки сопряжения (рис. 15, 17).

2.Внутренние – центры сопрягаемых дуг расположены по одну сторону от точек сопряжения (рис. 16, 18).

3.Смешенные – центр одной из сопрягаемых дуг лежит внутри сопрягающей дуги, а центр другой сопрягаемой дуги – вне неё (рис. 19)

Сопряжение дуги окружности и прямой линии дугой заданного радиуса. Внешнее сопряжение (рис. 15). Центр О ₁ дуги сопряжения (центр сопряжения) находится на пересечении вспомогательной прямой b, отстоящей от заданной прямой на величину радиуса r и параллельной ей, и вспомогательной дуги радиуса R+ r проведенной из центра О. Точки сопряжения С₃ и С₂ находятся соответственно в основании перпендикуляра О₁С₃ и на пересечении прямой ОО₁ с основной окружностью.

Внутреннее сопряжение (рис. 16). Центр О₁ дуги сопряжения (центр сопряжения) находится на пересечении вспомогательной прямой, отстоящей от заданной прямой на величину радиуса r, а также параллельной ей и дуги радиуса R- r проведенной из центра О. Точки сопряжения – соответственно в основании перпендикуляра ОС₁ и на пересечении продолжении луча ОО₁ с основной окружностью.

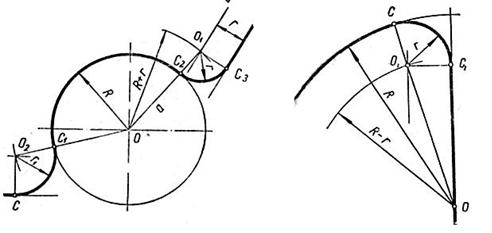
Рисунок 15. Внешнее сопряжение Рисунок 6. Внутреннее сопряжение

Сопряжение двух окружностей дугой заданного радиуса. Внешнее сопряжение (рис. 17). Центр сопряжения О₂ искомой дуги радиуса R находится на пересечении вспомогательных окружностей, описанных из центров О₁ и О соответствующими радиусами R + R₂ и R + R₁. Точки сопряжения S и S₁ лежат на пересечении прямых ОО₂ и О₁О₂ с основными окружностями соответственно.

Внутреннее сопряжение (рис. 18). Центр сопряжения О₂ искомой дуги радиуса R находится на пересечении вспомогательных окружностей, описанных из центров О и О₁ соответствующими радиусами R – R₂ и R – R₁ Точки сопряжения S и S₁ лежат на пересечении продолжения прямых ОО₂ и О₁О₂ с основными окружностями соответственно.

Смешанное касание (внешнее и внутреннее) (рис. 19). Центр сопряжения О₂ искомой дуги радиуса R находится на пересечении вспомогательных дуг, проведенных из центров О₁ и О соответствующими радиусами R – R₂ и R₁ + R. Точки сопряжения S₁ и S лежат на пересечении прямой ОО₂ и продолжении прямой О₁О₂ с основными окружностями соответственно.

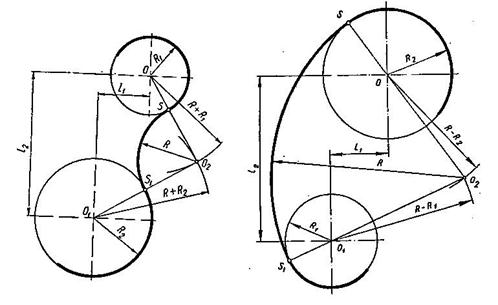
Рисунок 17. Внешнее сопряжение Рисунок 18 Внутреннее сопряжение

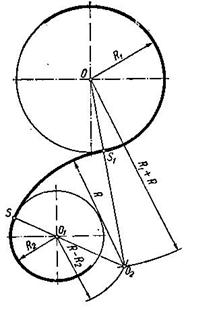
Рисунок 19. Смешанное касание

Сопряжение двух неконцентрических дуг окружностей третьей дугой заданного радиуса (рис.20). Центр О₃ дуги R₃ находится на пересечении двух вспомогательных дуг, построенных соответственно из центров О₁ и О₂ радиусами R₁+R₃ и R₂-R₃. Точки сопряжения К и М лежат на лучах соединяющих центры сопрягаемых окружностей.

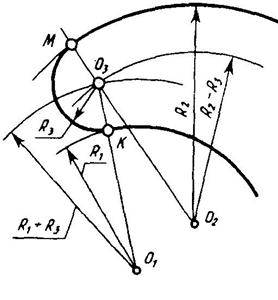
Рисунок 20. Сопряжение концентрических дуг

Вопросы для самоконтроля

1. Способы нанесения размеров отверстий, расположенных на одной оси.

2. Какие основные типы линий употребляются в черчении?

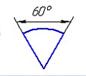
1. На каком рисунке правильно нанесен угловой размер?

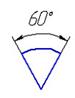
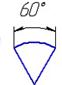
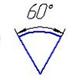
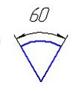
1. Выполнение и обозначение уклонов и конусности на чертежах. Приведите примеры.

1. Как определяются центр и точки сопряжений? Приведите примеры.
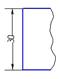
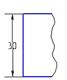
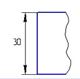
2. На каком рисунке правильно проставлен размер?

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Лагерь А.И. Инженерная графика / А.И. Лагерь. - М.: Высшая школа, 2002 – 270 с.

2. Фазлулин Э.М., Халдинов В.А. Инженерная графика / Э.М. Фразулин, В.А. Халдинов. - М.: Издательский центр «Академия», 2008 – 400 с.

3. Чекмарев А.А. Инженерная графика / А.А. Чекмарев. - М.: Высшая школа, 2002 – 365 с.

Дополнительная

1. ГОСТы ЕСКД.

2. Герасимов А.Г., Болынова В.В., Марьина А.А.. Сопряжения. Лекальные кривые / А.Г. Герасимов, В.В. Болынова, А.А. Марьина; ФГОУ ВПО «Саратовский ГАУ». – Саратов, 2008. – 20 с.

3. Левицкий В.С. Машиностроительное черчение и автоматизация выполнения чертежей / В.С. Левицкий. - М., Высшая школа, 2000 г.

4. Чекмарев А.А. Задачи и задания по инженерной графике / А.А. Чекмарев. - М.: ИЦ «Академия», 2008 – 128 с.

Дата добавления: 2014-01-07