Тема 6. Модели систем массового обслуживания

Системами массового обслуживания (СМО) называются системы специфического вида, предназначенные для обслуживания потока заявок (требований). Заявки на обслуживание поступают в систему нерегулярно, в заранее неизвестные и случайные моменты времени. Примеры заявок: покупатели, приходящие в магазин; клиенты в парикмахерской, телефонные вызовы в сети; телевизоры, поступающие в мастерскую на ремонт. Обслуживание заявок выполняют каналы обслуживания (обслуживающие устройства). Примеры каналов обслуживания: продавец в магазине, кассир за кассой, мастер в телеателье, парикмахер и т.д. Обслуживание заявок каналом имеет также случайный характер: время обслуживания каждой заявки является случайной величиной и зависит от многих факторов (например, от характера поломки аппарата зависит время его ремонта, от запросов и возраста покупателя – время его обслуживания продавцом и т.д.)

Случайный характер потока заявок и времени их обслуживания обуславливает неравномерность загрузки системы: на входе могут накапливаться не обслуженные заявки (перегрузка СМО), либо заявок нет, и каналы простаивают.

Структура системы массового обслуживания может быть представлена в виде следующей схемы, показанной на рис. 6.1.

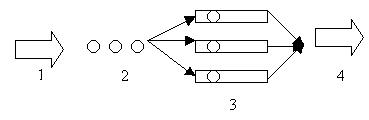
1-входной поток заявок;

2- очередь;

3 – каналы обслуживания

4 – выходной поток заявок

5 – заявки, получившие отказ в обслуживании.

Рис.6.1. Структура системы массового обслуживания.

Целью теории массового обслуживания является выработка рекомендаций по рациональному построению системы. Например, требуется определить рациональное число каналов обслуживания, при которых с одной стороны, не возникает бесконечных очередей и время ожидания в очереди является приемлемой величиной, а с другой – нет значительных простоев каналов, поскольку организация каждого канала связана с материальными затратами. Так, например, при организации торговли эти методы позволяют определить оптимальное количество торговых точек определенного профиля, численность продавцов, необходимые размеры торгового зала и другие параметры.

Классификация СМО:

1. По числу каналов обслуживания различают одноканальные, многоканальные и многофазные СМО. Если каналы выполняют параллельную обработку сразу нескольких заявок, то система называется многоканальной. (кассовые аппараты в магазине самообслуживания). В многофазной системе процесс обслуживания заявки состоит из нескольких этапов, выполняемых последовательно друг за другом на различных каналах обслуживания (партия изделий последовательно обрабатывается в ряде цехов).

2. По правилам обслуживания различают три класса СМО:

1) СМО с отказами -если нет свободных каналов, заявка покидает систему (не дозвонился)

2) СМО с ожиданием -если нет свободных каналов, заявка ожидает в очереди (торговля, поликлиника)

3) СМО с ограниченной длиной очереди – число мест для ожидания в очереди ограничено. Отказ в обслуживании происходит, если все каналы заняты и нет мест в очереди (автосервис).

3. По дисциплине очереди (способу отбора заявок из очереди на обслуживание) различают:

1) Очередь FIFO (Первый пришел - первый обслужен)

2) Очередь LIFO (Последний пришел – первый обслужен)

3) Очередь с приоритетом. Некоторые заявки на основании каких-то признаков получают преимущество (приоритет) в выборе на обслуживание перед другими. Например, ветераны и участники войны в поликлинике пропускаются без очереди.

4. По характеру входного потока заявок различают:

1) Замкнутые СМО, в которых обслуженная заявка через какой-то промежуток времени вновь возвращается в систему (отремонтированный станок в цеху опять ломается, посуда в общественной столовой опять загрязняется и т.д.).

2) Разомкнутые (открытые) СМО, в которых входящий поток заявок не зависит от выходящего и ничем не ограничивается. (Заявки поступают в систему извне, от некоторого бесконечного источника заявок).

В настоящее время теоретически наиболее разработаны и удобны для практического применения системы массового обслуживания, которые называются простейшими. Простейшей системой массового обслуживания называется такая система, в которой:

1) входящий поток заявок является простейшим (пуассоновским);

2) время обслуживания заявки каждым каналом имеет экспоненциальный закон распределения.

Пуассоновский поток заявок обладает тремя основными свойствами:

1) ординарность означает, что практически невозможно одновременное поступление двух и более заявок. (невозможен одновременный выход из строя двух станков, одновременный приход двух покупателей и т.д.).

2) стационарность означает, что среднее число заявок, поступающих в единицу времени, постоянно. Таким образом, хотя заявки и поступают в случайные моменты времени, в среднем поток является равномерным.

Обозначим:

- среднее число заявок, поступающих в систему в единицу времени.

(например, среднее число телевизоров, поступающих в ремонтную мастерскую за день)

3) отсутствие последействия означает, что количество заявок, уже поступивших в систему, не определяет того, сколько заявок поступит далее. (Например, если произошел обрыв нити на ткацком станке, то это не означает, что его не будет в следующий момент времени, и, тем более, что его не будет на других станках).

Экспоненциальный закон времени обслуживания заявок имеет параметр 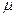, который обозначает среднее число заявок, которое может обслужить один канал за единицу времени. Например, 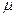- это среднее число телевизоров, которые может отремонтировать один мастер за день. Величина 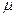обратно пропорциональна среднему времени обслуживания одной заявки Т_об:

.

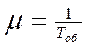Для простейшей СМО всегда рассчитывается величина

.

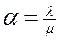Если рассматривается система с ожиданием в очереди, причем размер очереди не ограничен, то 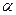имеет следующий смысл: это среднее число каналов, которые необходимо иметь, чтобы обслуживать в единицу времени все поступающие заявки.

Пусть n - число имеющихся в системе каналов обслуживания. (например, число мастеров в телеателье). Тогда условие работоспособности простейшей СМО с ожиданием:

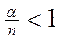Û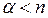

Т.е. число обслуживающих каналов должно быть больше средней величины 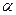. Если это условие выполняется, система является работоспособной. В случае нарушения этого условия каналы не будут справляться с обслуживанием всех заявок, очередь будет расти бесконечно, и система просто захлебнется в потоке заявок.

При оценке качества работы СМО кроме этого основного показателя, рассчитываются ряд других показателей эффективности работы системы:

1) Среднее время ожидания начала обслуживания (время пребывания в очереди);

2) Средняя длина очереди;

3) Вероятность того, что все обслуживающие каналы заняты в момент поступления нового требования в систему;

4) Среднее число свободных от обслуживания каналов;

5) Коэффициенты занятости каналов обслуживания;

6) И т.д.

При этом некоторые из этих показателей более интересны с точки зрения клиента (1,2,3), а другие – с точки зрения владельца мастерской (4,5). Величина средней длины очереди важна для расчета площадей складских помещений, предназначенных для хранения аппаратов, ожидающих ремонта.

Дата добавления: 2014-01-07