Тема 7. Матричные игры

Игрой называется математическая модель конфликтной ситуации, реализующейся в условиях неопределенности.

Например, при определении объема выпуска продукции на одном предприятии нельзя не учитывать размеров выпуска аналогичной продукции на других предприятиях. Однако невозможно полностью контролировать деятельность конкурентов, можно только предполагать возможные варианты их действий. Поэтому решение приходится принимать в условиях неопределенности. Каждое из конкурирующих предприятий преследует свои цели, поэтому имеет место конфликтная ситуация

Исследованием конфликтных ситуаций занимается раздел математики - теория игр. В игре могут сталкиваться интересы двух (игра парная) или нескольких (игра множественная) противников; существуют игры с бесконечным множеством игроков. По характеру выигрышей выделяют игры с нулевой суммой и с ненулевой суммой. В играх с нулевой суммой общий капитал игроков не изменяется, а лишь перераспределяется в ходе игры, поэтому сумма выигрышей равна нулю (проигрыш рассматривается как отрицательный выигрыш). В случае парной игры это означает, что выигрыш одного игрока равен проигрышу другого. В играх с ненулевой суммой сумма выигрышей отлична от нуля. Например, при организации лотереи часть общего взноса участников не участвует в формировании призового фонда, а идет организатору лотереи.

Мы будем рассматривать только парные игры с нулевой суммой.

Игры, в которых оба участника сознательно стремятся добиться для себя наилучшего результата, называются стратегическими. Часто игровой схемой формализуют такие ситуации, в которых один из участников безразличен к результату игры. Такие игры называют статистическими или играми с природой. Под термином “природа” понимают всю совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решение (погодные условия, спрос на рынке, состояние валютной биржи и т.д.). В играх с природой степень неопределенности при принятии решения сознательным игроком возрастает. “Природа”, будучи безразличной в отношении выигрыша, может реализовать такие стратегии, которые ей совершенно невыгодны, а выгодны сознательному игроку. Поэтому решение принять сложнее, а выиграть можно больше.

Особенность игр с природой в том, что решение достаточно найти только для сознательного игрока, поскольку природа никакие рекомендации воспринять не может. Как правило, игры с природой решаются на основании различных критериев.

Рассмотрим стратегическую парную игру с нулевой суммой. Игра ведется по определенным правилам. Каждый участник игры имеет несколько вариантов возможных действий (чистых стратегий). Из них он выбирает такие варианты, которые, как он полагает, могут обеспечить ему наилучший результат (исход игры). При этом каждый игрок имеет лишь представление о множестве допустимых ответных действий партнера, но не о его конкретном решении. Так что как одному, так и другому игроку решение приходится принимать в условиях неопределенности. Исход игры – это значение некоторой функции, называемой функцией выигрыша или платежной функцией. Эта функция задается либо аналитическим выражением, либо таблично, т.е. с помощью платежной матрицы. В последнем случае игра называется матричной.

Пусть в игре участвуют два игрока: A и B. Игрок А имеет m чистых стратегий A₁, A₂, …, A_m; а игрок B – n чистых стратегий B₁, B₂, …, B_n. По строкам в платежной матрице (табл.7.1.) располагаются стратегии игрока А, а по столбцам – стратегии игрока В. Элемент платежной матрицы a_ij, который находится на пересечении i –ой строки и j-го столбца, есть выигрыш игрока A (и в то же время проигрыш игрока B) в ситуации, когда игрок A выбрал стратегию A_i, а игрок B независимо от него выбрал стратегию B_j. Таким образом, именно независимый выбор двух игроков определяет исход игры (величину выигрыша игрока А).

Таблица 7.1. Платежная матрица игры.

	В1	...	Вn
А1	а11	...	а1n
A2	a21	...	a2n
…	...	...	...
Аm	am1	...	аmn

Например, в платежной матрице величина a₂₁ показывает выигрыш игрока А и, в то же время, проигрыш игрока В, если игрок А выбирает свою чистую стратегию А₂, а игрок В выбирает чистую стратегию В₁.

Пример 7.1. В игре принимают участие два игрока. Каждый из игроков может записать независимо от другого игрока число 4, 5 или 6. Если разность между числами, записанными игроками А и В положительна, то игрок А выигрывает количество очков, равное этой разности. Если разность отрицательна, то выигрывает игрок В. Если разность равна нулю, то игра заканчивается вничью.

Составим платежную матрицу игры. У игрока А имеется три стратегии:

A₁ – записать число 4

А₂ – записать число 5

А₃ – записать число 6

Поэтому платежная матрица будет иметь три строки.

Аналогично игрок В имеет три стратегии: B₁, B₂, B₃ (записать 4, 5 или 6 соответственно). Платежная матрица имеет три столбца.

В случае, если игрок А запишет 4 (стратегия А₁), а игрок В запишет также 4 (стратегия В₁), то выигрыш игрока А составит 4-4=0, т.е. элемент платежной матрицы а₁₁=0.

Если же игрок А выберет стратегию А₃ (запишет число 6), а игрок В выберет стратегию В₁ (запишет число 4), то выигрыш игрока А составит а₃₁=6-4=2. Столько же проиграет игрок В.

Аналогично рассчитываются все остальные элементы платежной матрицы.

Отрицательный выигрыш означает на самом деле проигрыш. Так, а₂₃= -1 означает, что если игрок А выберет стратегию А₂ (запишет 5), а игрок В выберет стратегию В₃ (запишет 6), то А выиграет –1 очко (т.е. проиграет 1 очко), а В проиграет –1 очко (т.е. выиграет 1 очко).

Платежная матрица данной игры имеет вид, показанный в табл.7.2.

Таблица 7.2. Платежная матрица примера.

	B1 (4)	B2 (5)	B3 (6)
A1 (4)		-1	-2
A2 (5)			-1
A3 (6)

Принцип минимакса.

Пусть дана парная игра с нулевой суммой, заданная платежной матрицей размерности m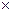n. Решить матричную игру означает определить наилучшую стратегию игрока A, а также наилучшую стратегию игрока B. Если рассматривается стратегическая игра, то предполагается, что противники одинаково разумны, и каждый из них делает все для того, чтобы добиться своей цели. Поэтому каждый игрок должен рассчитывать на самое неблагоприятное для себя поведение противника.

Используя этот принцип, найдем наилучшую стратегию игрока A. Выбирая стратегию A_i, мы должны рассчитывать, что игрок B ответит на нее той из своих стратегий B_j, для которой выигрыш игрока A будет минимальным. Поэтому для каждой стратегии Ai найдем

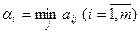
где– минимальный гарантированный выигрыш игрока А при применении стратегии Аi.

Очевидно, что желающий перестраховаться игрок A должен предпочесть другим стратегиям ту, для которой гарантированный выигрыш максимален. Обозначим

.

Величина 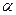называется нижней ценой игры или максимином. Стратегия, обеспечивающая игроку A получение нижней цены игры, называется максиминной стратегией. Если игрок А будет придерживаться своей максиминной стратегии, то ему гарантирован выигрыш, не меньший нижней цены игры при любом поведении игрока В.

Аналогично, определим наилучшую стратегию игрока В. С его точки зрения, в платежной матрице записаны проигрыши. Он заинтересован уменьшить свой проигрыш. Поэтому в каждом из столбцов (соответствующем определенной стратегии) он должен найти максимальное значение проигрыша при выборе стратегии B_j:

Выбирать стратегию игроку B следует так, чтобы минимизировать величину проигрыша при любых действиях соперника, т.е. обеспечить 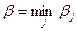. Величина

называется верхней ценой игры (минимаксом), а соответствующая ей чистая стратегия B_j – минимаксной. Если игрок В будет придерживаться своей минимаксной стратегии, то ему гарантировано, что в любом случае он проиграет не больше верхней цены игры.

Можно показать, что всегда максимин не превосходит минимакс, т.е.

.

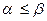Если нижняя цена игры равна верхней (a=b), то говорят, что игра имеет седловую точку и чистую цену игры g=a=b. Стратегии A_i^* и B_j^*, позволяющие достичь этого значения, называются оптимальными, а пара оптимальных стратегий (А_i^*,В_j^*), называется седловой точкой матричной игры.

Таким образом, решив игру с седловой точкой, мы рекомендуем каждому игроку применять одну свою стратегию (A_i^* или B_j^*). Тогда игроку А гарантировано, что он получит выигрыш, не меньший чистой цены игры g. Игроку В гарантировано, что он получит проигрыш, не больший чистой цены игры g.

Пример 7.2. Найдем решение игры предыдущего примера. Добавим к платежной матрице дополнительный столбец справа и дополнительную строку снизу, как показано в табл.7.3.

Таблица 7.3. Выбор оптимальных стратегий по принципу минимакса.

	B1 (4)	B2 (5)	B3 (6)
A1 (4)		-1	-2	-2
A2 (5)			-1	-1
A3 (6)			0*

Если игрок А выбирает чистую стратегию A₁ (записывает число 4), то его минимальный выигрыш составит

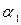=min(0; -1; -2) = -2.

Аналогично находятся значения 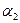и 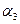(см. последний столбец). Наибольший из минимальных выигрышей стратегий (нижняя цена игры):

.

Нижней цене игры соответствует стратегия А₃. Таким образом, если игрок А выбирает стратегию А₃ (записывает число 6), то ему гарантирован выигрыш, не меньший .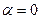

Если игрок В выбирает чистую стратегию В₁ (записывает 4), то его максимальный проигрыш:

=max(0, 1, 2)=2.

Аналогично находим максимальный проигрыш для столбцов 2 и 3 (см. последнюю строку). Наименьший из максимальных проигрышей (верхняя цена игры):

.

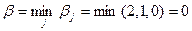Верхней цене игры соответствует стратегия В₃. Таким образом, если игрок В выбирает стратегию В₃ (записывает число 6), то ему гарантирован проигрыш, не больший .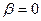

Поскольку , то игра имеет седловую точку и решение в чистых стратегиях. Чистая цена игры 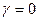. Оптимальная стратегия игрока А - A₃. Оптимальная стратегия игрока B - B₃. Игрокам рекомендуется выбирать свои оптимальные стратегии.

Дата добавления: 2014-01-07