
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дисконтирование денежных потоков
|
|
|
|
ТЕМА 9. МОДЕЛИ АНАЛИЗА ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
Метод дисконтирования денежных потоков является ключевым в финансовом анализе. Рассмотрим этот метод на примере банковских депозитов. Обозначим:
P – начальный капитал, положенный в банк;
r – процентная ставка банка;
S – наращенная сумма.
Тогда в конце первого периода капитализации наращенная сумма составит:
 .
.
Если эта сумма остается в банке, то в конце второго периода капитализации наращенная сумма составит:
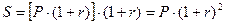 .
.
В общем случае сумма, наращенная за n периодов капитализации, рассчитывается по формуле:
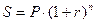 . (9.1)
. (9.1)
В течение периода капитализации проценты могут начисляться несколько раз, тогда наращенная сумма будет увеличиваться.
На основании формулы (9.1) можно также найти, какой начальный капитал нужно положить в банк, чтобы наращенная за n периодов капитализации сумма составила заданную величину S. Такой начальный капитал называется текущей (приведенной) ценностью суммы S и обозначается PV:
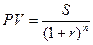 . (9.2)
. (9.2)
Процесс нахождения текущей ценности называется дисконтированием.
Пример 9.1. Годовая процентная ставка банка составляет 12%. Какую сумму нужно положить в банк, чтобы наращенная за пять лет сумма составила 1000 ден. единиц?
Решение. По условию r =0,12; n =5; S =1000. По формуле (9.2) найдем текущую ценность заданной суммы:
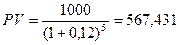 .
.
Таким образом, в банк следует положить 567,431 ден. ед.
На основании формулы (9.1) можно также решить задачу определения количества времени, требующегося для накопления определенной суммы.
Пример 9.2. Если положить в банк 1000 у.е. при годовой процентной ставке 10%, то через сколько лет накопленная сумма составит 2000 у.е.?
Решение. По условию даны следующие величины: P =1000; S =2000; r =0,1. Требуется найти количество временных периодов n. Запишем формулу (9.1): 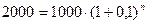 . Решив это уравнение относительно n, получим: n=7,27. Таким образом, на данное накопление потребуется больше семи лет.
. Решив это уравнение относительно n, получим: n=7,27. Таким образом, на данное накопление потребуется больше семи лет.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 428; Нарушение авторских прав?; Мы поможем в написании вашей работы!