Решение

Результаты расчетов основных показателей динамики представлены в таблице:

Год	Выпуск продукции, млн.руб.	, 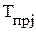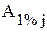млн.руб.	, %	, %	, млн.руб.
ц	б	ц	б	ц	б
	103,0	-	-			-	-	-
	105,4	2,4	2,4	102,3	102,3	2,3	2,3	1,03
	107,4	2,0	4,4	101,9	104,3	1,9	4,3	1,054
	110,7	3,3	7,7	103,1	107,5	3,1	7,5	1,074
	109,0	-1,7	6,0	98,5	105,8	-1,5	5,8	1,107
	107,3	-1,7	4,3	98,4	104,2	-1,6	4,2	1,09

Среднее значение уровня интервального ряда динамики с равно-отстоящими уровнями рассчитывается по формуле средней арифметической простой:

млн.руб.

Средний абсолютный прирост:

млн.руб.

Средний темп роста:

.

Средний темп прироста:

.

Прогноз объема производства продукции на ближайшие три года осуществляется с помощью модели, построенной на основе среднего темпа роста:

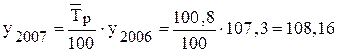млн.руб.,

млн.руб.,

млн.руб.

7.2. Одной из основных задач статистики при анализе ряда динамики является выявление основной тенденции развития (тренда) изучаемого социально-экономического явления. Тенденция (тренд) характеризует общее направление развития явления под действием основных факторов, исключая влияние случайных факторов, вызывающих колебания уровней относительно тренда. Существуют различные методы и способы позволяющие выявить основную тенденцию ряда динамики, но наиболее эффективным из них является аналитическое выравнивание ряда динамики. Согласно этому методу происходит выравнивание каждого значения уровня ряда динамики по формуле, имеющей общий вид:

,

где 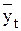- выровненные значения уровней ряда динамики;

- аналитический вид функции выравнивания.

В качестве функции выравнивания может использоваться парабола, гипербола, синусоида, степенная, логарифмическая или линейная функции. Рассмотрим механизм выравнивания ряда динамики по прямой.

В общем виде уравнение прямой можно представить следующим образом:

,

где , - коэффициенты уравнения выравнивания;

- порядковый номер временного показателя.

Для построения уравнения выравнивания необходимо определить значения коэффициентов , . Коэффициенты уравнения выравнивания рассчитываются по методу наименьших квадратов из системы двух уравнений вида:

.

Порядковый номер временного показателя выбирается таким образом, чтобы выполнялось условие 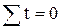. При этом возможны две ситуации. Первая − ряд динамики имеет нечетное количество уровней, например:

Год
t	-2	-1

Вторая − ряд динамики имеет четное количество уровней, например:

Год
t	-5	-3	-1

Тогда, система уравнений примет вид:

.

Откуда, коэффициенты определяются по формулам:

.

Построенное уравнение прямой позволяет определить выровненные значения уровней ряда динамики, а его визуальный анализ − выявить основную тенденцию развития изучаемого социально-экономического явления (возрастание, убывание изучаемого признака или его неизменность с течением времени).

По окончанию процедуры выравнивания ряда динамики необходимо убедиться, насколько точно выровненный ряд описывает изучаемое социально-экономическое явление. Для этого определяют коэффициент вариации по формуле:

,

где 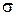- среднее квадратическое отклонение;

- среднее значение уровня выровненного ряда динамики.

Среднее квадратическое отклонение определяется по формуле:

,

где , - соответственно исходные и выровненные значения уровней ряда динамики.

Чем меньшее значение имеет коэффициент вариации, тем более точно выровненный ряд динамики описывает изучаемое социально-экономическое явление и, наоборот. При неудовлетворительно большом значении коэффициента вариации делается вывод о том, что построенное уравнение выравнивания неадекватно описывает изучаемое социально-экономическое явление, а анализ выровненного ряда динамики не позволяет выявить основную тенденцию его развития. В этом случае рекомендуется выравнивать ряд динамики по другой функции, дающей более предпочтительный результат.

Уравнения выравнивания, построенные по другим функциям, представлены в табл. 7.1.

Таблица 7.1

Уравнения выравнивания, построенные по другим функциям

Функция выравнивания:	Формулы определения коэффициентов уравнения выравнивания
- парабола	, ,
- гипербола	,
- показательная	,
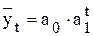
- ряд Фурье	, ,

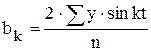
Уравнение выравнивания, адекватно описывающее изучаемое социально-экономическое явление, может быть использовано в прогнозных расчетах. Например, прогнозная модель, построенная на основе линейного уравнения выравнивания, имеет вид:

,

где - прогнозное значение уровня ряда динамики для периода с порядковым номером (t+j);

- порядковый номер для прогнозируемого периода.

Пример 7.2. По данным о производстве продукции на предприятии за 5 лет выявить основную тенденцию развития производства (исходные данные в 1 и 2 столбцах таблицы). Спрогнозировать объем производства продукции на ближайшие три года, используя модель, построенную на основе линейного уравнения выравнивания.

Дата добавления: 2014-01-07