Частотные характеристики звеньев

Важными частотными характеристиками звена являются частотные характеристики, которые определяют взаимосвязь между параметрами гармонических сигналов на входе и выходе в установившемся (вынужденном) режиме.

Основная частотная характеристика – амплитудно-фазовая характеристика (АФХ). Ее выражение получают заменой p на 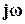в ПФ W(p):

.

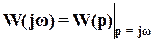Выражение для АФХ - функция комплексной переменной. Поэтому это выражение можно представить в показательной и алгебраической формах:

.

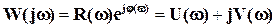При этом получаем еще 4 частотных характеристики:

Амплитудно-частотную характеристику (АЧХ) звена

R(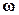)=mod W(j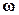)=|W(j)|.

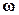Фазо-частотную характеристику (ФЧХ) звена

.

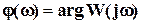Вещественную частотную характеристику звена

U(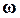)=ReW(j).

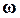Мнимую частотную характеристику звена

V(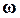)=JmW(j).

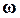Для исследования частотных свойств звеньев и систем удобно использовать графическое представление частотных характеристик.

Определение. Годограф W(j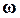), построенный на комплексной плоскости

(U, jV) при изменении w от 0 до 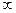, также называется АФХ звена.

Выражение для АФХ имеет свойство:

W(-j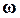)=W*(j),

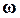где * - символ комплексно-сопряженного выражения, отсюда

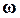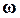U(-)=U(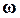), V(-)=-V().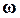

Поэтому не строят ветвь годографа W(j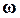), соответствующую отрицательным частотам, т.к. эта ветвь является зеркальным отображением АФХ относительно вещественной оси. Однако в зарубежной литературе широко используют годограф W(j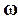), построенный для диапазона частот -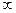≤≤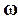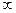, и называемый диаграммой Найквиста.

Физический смысл АФХ: Она определяет установившуюся (вынужденную) реакцию звена на гармонический входной сигнал. При этом АЧХ R(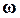) определяет амплитуду, а ФЧХ 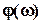определяет фазу установившейся реакции на гармонический сигнал с частотой .

Пример.Matlab 6.5 Новая папка2/bandwidth_demo.m

Логарифмические частотные характеристики (диаграммы Боде)

Анализ и синтез САУ удобно выполнять, используя логарифмические частотные характеристики (ЛЧХ), что объясняется простотой их построения.

ЛЧХ называют построенные в логарифмическом масштабе частотные характеристики R( ) и 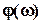. Для фиксированной частоты значение R( ) – отношение амплитуд гармонических сигналов на входе и на выходе звена. Если на входе и выходе сигналы одной физической природы, то

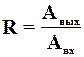
есть натуральное число, показывающее во сколько раз больше амплитуда выходного сигнала Авых, чем амплитуда входного сигнала Авх. Это число может с изменением частоты изменяться в очень широких пределах, что создает трудности при построении ЛЧХ. Поэтому в качестве единицы измерения используют такую единицу измерения как децибел (дБ). Число R, выраженное в децибелах, определяется так:

L=20lgR [дБ].

Значения ФЧХ при построении ЛЧХ обычно измеряют в градусах или радианах.

Дадим определение ЛЧХ с учетом замечаний относительно единиц измерения.

Определение. Логарифмической амплитудно-частотной характеристикой (ЛАЧХ) называют график зависимости L(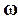)=20lgR(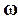), построенный в логарифмическом масштабе частот lg.

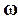Определение. Логарифмической фазо-частотной характеристикой называется график зависимости 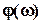, построенный в логарифмическом масштабе частот lg.

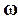Построение логарифмической оси частот

Возьмем частоты, кратные десяти:

=

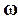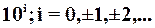
Найдем lg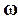=i и на оси абсцисс отложим значения lg, а около засечек запишем значения самой частоты (см. рисунок) Если теперь уберем с оси значения lg , то получим логарифмическую ось частот.

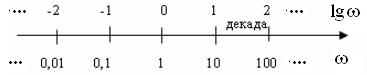
Как видим, логарифмическая ось равномерна относительно частот, кратных 10.

Так же можно получить точки на оси частот для частот, некратных 10, например: =2, lg2=0,3.

Говорят, что если частота изменилась в 10 раз, то она изменилась на декаду, т.е. логарифмическая ось фактически разбита на декады.

Размерность угловой частоты: 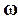[рад/с] записывают как [].

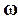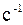Частотные характеристики звеньев должны начинаться с какой-то частоты. Логарифмическая ось частот начинается в бесконечности, т.к. логарифм нуля не существует.

Поэтому обычно ось ординат проводится на такой частоте, чтобы все характерные особенности ЛЧХ оказались справа от этой оси.

Дата добавления: 2014-01-07