Апериодическое звено 1-ого порядка

Лекция 7

Другое название непериодическое или неколебательное звено. Так называется по виду временных характеристик. Иногда называют инерционным. Относится к числу динамических звеньев. Все динамические звенья не сразу реагируют на изменение входного сигнала.

Заметим, что CАУ первого порядка в отсутствие возмущений и шума измерений описывается моделью в виде апериодического звена.

а) Уравнение и ПФ

Уравнение звена находим из

(*)

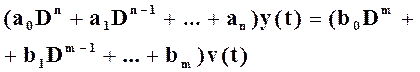при n=1, m=2:

(a₀D+a₁)y(t)=b₀v(t),

где a₀ >0, b₀ >0, a₁ >0.

Делим это уравнение на a₁, получаемуравнение звена в стандартной форме

(TD+1)y(t)=k v (t),

где параметры звена

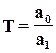- постоянная времени; 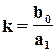- коэффициент усиления звена; T>0 и k>0.

Поясним, почему T называется постоянной времени. Если выходной сигнал звена является напряжением и измеряется в вольтах, y [B], то все члены уравнения должны иметь ту же размерность. Отсюда TDy(t)=T(t) [B]. Так как размерность скорости изменения выходного сигнала [B/c], следовательно, постоянная времени T измеряется в секундах [c].

Выясним физический смысл коэффициента усиления k. Для этого введем понятие состояния равновесия звена. Приложим на вход звена постоянный сигнал v(t)= 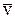=const. В состоянии равновесия все производные от входа и выхода равны нулю, так что при v(t)= 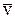=const получаем y(t)= =const. Следовательно, в состоянии равновесия (в установившемся состоянии)

=k,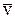

k=/.

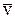Таким образом, k – коэффициент усиления, связывающий между собой вход и выход звена в состоянии равновесия.

Рассмотрим невозбужденное звено. Тогда уравнение звена в изображениях:

(Tp+1)y(p)=kv(p).

Отсюда передаточная функция апериодического звена

W(p)= y(p)/ v(p)=k/(Tp+1)

б) Временные характеристики

Весовая функция по определению w(t)= L^-1[k/(Tp+1)]. Отсюда

Переходная характеристика:

h(t)= L^-1[k/(p(Tp+1))],

h(t)=k(1- )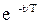

при t≥0. Для t<0 h(t)=0.

Переходную характеристику (см. рисунок ниже) можно представить как сумму

двух составляющих

h(t)=hуст(t)+hпер(t),

где установившееся значение переходной характеристики

hуст(t)=h(∞) =k,

переходной процесс (см. рис. ниже)

hпер(t)= -k .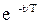

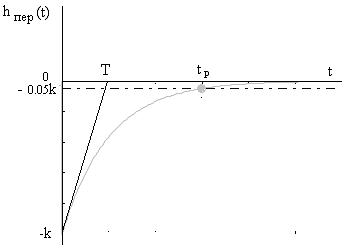
Процесс перехода из нулевого установившегося состояния в другое установившееся состояние называется переходным процессом. Для апериодического звена он затухает теоретически через бесконечно большой

промежуток времени.

Практически длительность переходного процесса определяется моментом времени, начиная с которого переходная характеристика удовлетворяет условию

│h(t) - hуст│< λ hуст _,

где λhуст – допустимая ошибка. Значение λ выбирается в пределах 0.01÷0.05. Как правило, принимают λ =0.05, другими словами, считают, что переходный процесс закончился, если переходная характеристика отличается от установившегося значения не более, чем на 5%, т.е., как говорят, определяют значение tp при 5% допустимой ошибке. При этом практическая длительность переходного процесса для апериодического звена:

tp=3T.

Как видим, постоянная времени определяет быстродействие звена, чем выше T, тем выше инерционность звена, чем ниже T, тем инерционность ниже.

Использовать Kybsim/first_order_system.exe.

в) Частотные характеристики звена

АФХ. По определению

W(jω)=W(p) │p=jω.

ПФ для апериодического звена

W(p)=k/(Tp+1),

тогда

W(jω)=k/(jωT +1)

при k>0.

Найдем АЧХ звена:

R(ω)=k/.

.

Найдем ФЧХ звена:

φ(ω)=arctg(ωT).

Это звено представляет собой фильтр низких частот (ФНЧ).

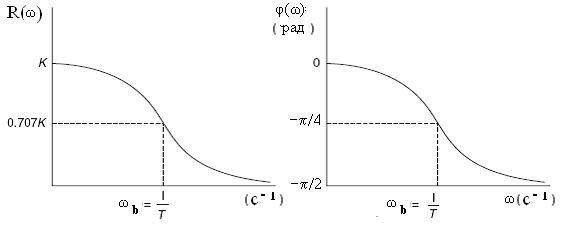
Полоса пропускания (0, ω_b) на уровне 0, 707 определяется как

ω_b=1/T.

Выясним какое влияние оказывает полоса пропускания на быстродействие звена. Т.к. tp=3T, то практическая длительность переходного процесса при 5% допустимой ошибке равна

tp=3/ω_b.

Чем выше полоса пропускания, тем выше быстродействие звена и тем ниже его инерционность.

Построим АФХ в виде годографа на комплексной плоскости (см. рис. ниже). АФХ представляет собой полуокружность с радиусом k/2 и центром в точке (k/2, j0):

W(jω)=U+jV=(k/2)*[1+ ].

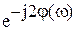Рассмотрим логарифмическую амплитудно-частотную характеристику звена (ЛАЧХ). По определению

L(ω)=20lgR(ω)=20lgk-20lg .

Удобнее строить асимптотическую характеристику

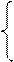20lgk, ω≤1/T,

La(ω) =

20lgk - 20lg ωT, ω≥1/T,

состоящую из 2 – х асимптот.

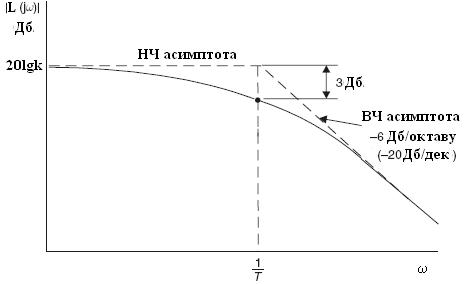
Необходимо знать одну точку и наклон прямой для построения высокочастотной асимптоты. Наклон высокочастотной асимптоты в логарифмическом масштабе частот определяется как

, Q = lgω.

Если ω=1/T, то La(ω)=20lgk. Таким образом, при этой частоте высокочастотная асимптота проходит через точку с ординатой 20lgk.

Другой способ определения наклона высокочастотной асимптоты: изменим частоту на декаду(в 10 раз)

La(10ω)- La(ω)=20lgk-20lg10ωT-20lgk+20lgωT=-20дБ.

Наклон: -20 дБ/дек.

Построим точную и асимптотическую ЛАЧХ: ω=1/T – сопрягающаяся

частота. Как видим, асимптотическая L(ω)≈La(ω) (max отличие между ними – 3 дБ)

Рассмотрим точную и асимптотическую ЛФЧХ - φ(ω) в логарифмическом масштабе частот.

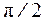Если частота достаточно большая, то звено сдвигает фазу гармонического сигнала на -градусов.

При определенных условиях можно считать апериодическим звеном систему АУ.

Дата добавления: 2014-01-07