Колебательное звено. Заметим, что CАУ второго порядка в отсутствие возмущений и шума измерений описываются моделью в виде колебательного звена

Заметим, что CАУ второго порядка в отсутствие возмущений и шума измерений описываются моделью в виде колебательного звена.

а) Уравнение и передаточная функция

Дифференциальное уравнение звена 2-ого порядка (n=2, m=0):

.

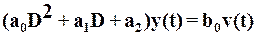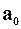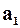Пусть >0, >0, 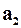>0. Приводим уравнение к стандартному виду (делим на ):

,

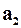где 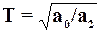- постоянная времени, 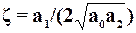- относительный коэффициент затухания и 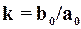- коэффициент усиления звена 2-го порядка. Параметры звена: 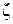, T и k. Также как для апериодического звена k – коэффициент усиления, связывающий между собой вход и выход звена 2-го порядка в состоянии равновесия.

Есл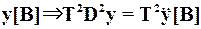и , и .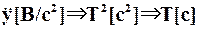

При 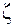>1 звено наз. апериодическим звеном 2-ого порядка, при 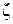=0 – консервативное звено, при 0<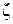<1 – колебательное звено.

Иногда уравнение звена 2-ого порядка записывают в другом виде

,

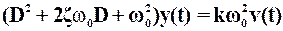где 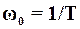- частота собственных колебаний.

Уравнение колебательного звена в изображениях после преобразования Лапласа:

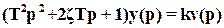
или

.

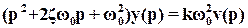Отсюда ПФ колебательного звена (0<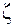<1)

,

.

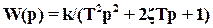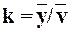б) Временные характеристики.

Весовая функция w(t)= L^-1[W(p)]. Используя таблицу преобразования Лапласа

.

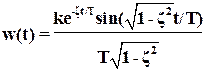Переходная характеристика: h(t)= L^-1[W(p)/p],

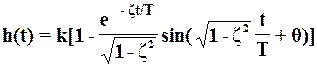, =arcos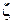

Вид переходной характеристики целиком определяется 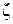(см. рис. ниже).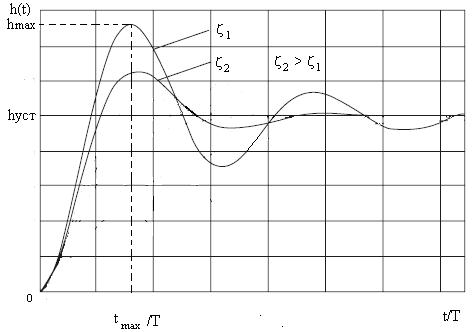

Если уменьшается 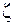, тем более колебательный характер имеет переходная характеристика. Если 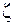=0, то имеют место незатухающие колебания.

Колебательность звена также характеризуется max выбросом h(t) относительно установившегося значения hуст=h(∞)=k. Этот выброс имеет место при

.

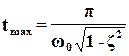Подставляя это значение в выражение для h(t), можно определить

относительный максимальный выброс

,

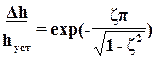который полностью определяется 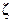. Здесь - абсолютный максимальный выброс.

Для САУ вводится понятие “перерегулирования” – это относительный максимальный выброс, выраженный в процентах

.

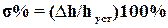Если САУ описывается моделью в виде колебательного звена, легко определить перерегулирование.

При 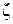=0 переходная характеристика имеет вид незатухающего колебания с частотой 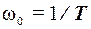, амплитудой k и постоянной составляющей k (консервативное звено). Такое название обусловлено тем, что кол-во энергии в звене остается неизменным, переходит из одного вида в другой (из потенциальной в кинетическую и наоборот).

Дата добавления: 2014-01-07