
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 9. 6. Форсирующее звено первого порядка
|
|
|
|
6. Форсирующее звено первого порядка.
Форсирующим звеном первого порядка называется звено, дифференциальное уравнение которого имеет вид:
 .
.
Нетрудно убедиться в том, что это выражение можно представить как сумму уравнений усилительного (пропорционального) и дифференцирующего звеньев.
Передаточную функцию форсирующего звена

принято записывать в стандартной форме
W(p)=k(1+Tp),
где k=k1 – коэффициент усиления, а T=k2/k1 – постоянная времени звена.
Передаточная функция форсирующего звена содержит полином в числителе, корень которого z=-1/T называется «нулем» форсирующего звена.
Переходная характеристика форсирующего звена определяется соотношением
 .
.
Качественный вид ее приведен на рис. ниже.

Весовая функция звена следующая:
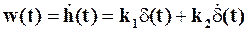
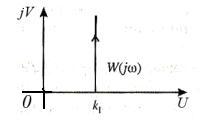
Амплитудно-фазовая характеристика находится по передаточной функции и имеет вид
W(j  )=k(1+jT
)=k(1+jT  ). (36)
). (36)
Соответствующая амплитудно-фазовая характеристика изображена на рисунке ниже.
Вещественная частотная характеристика звена не зависит от частоты и равна U(  )=k, мнимая частотная характеристика представляет собой прямую V(
)=k, мнимая частотная характеристика представляет собой прямую V(  )=kT
)=kT  .
.
Амплитудная частотная характеристика может быть построена по выражению
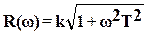 ,
,
а фазовая частотная характеристика определяется в виде
 (*)
(*)
причем в пределе  .
.
На основании выражения для R(  ) определим логарифмическую амплитудную частотную характеристику
) определим логарифмическую амплитудную частотную характеристику
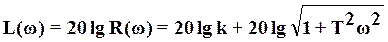 (**)
(**)
Как и в предыдущем случае, для форсирующего звена удобнее строить не точную, а асимптотическую ЛАЧХ. Здесь  0=1/T – сопрягающая частота звена.
0=1/T – сопрягающая частота звена.

Причем ее можно получить, исследуя отдельно области низких и высоких частот или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.
Нетрудно убедиться, сравнивая выражения
 и
и 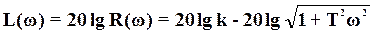 для ЛАЧХ и ЛФЧХ апериодического звена с выражениями (*) и (**), в том, что логарифмические амплитудная и фазовая частотные характеристики форсирующего звена представляют собой зеркальное отображение относительно оси абсцисс соответствующих логарифмических характеристик апериодического звена.
для ЛАЧХ и ЛФЧХ апериодического звена с выражениями (*) и (**), в том, что логарифмические амплитудная и фазовая частотные характеристики форсирующего звена представляют собой зеркальное отображение относительно оси абсцисс соответствующих логарифмических характеристик апериодического звена.
7. Форсирующее звено 2-го порядка
ПФ: 
При k=1 ЛЧХ – зеркальные отображения ЛЧХ колебательного звена относительно оси частот.
Форсирующие звенья, как первого, так и второго порядка физически неосуществимы.
8. Минимально-фазовые звенья
В общем случае передаточная функция звена
 ;
;
где
k’=b0/a0 - приведенный коэффициент усиления;
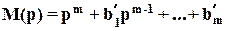 ;
; 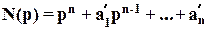 ;
;
 .
.
По теореме Безу:

Здесь zj,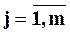 - нули ПФ; si,
- нули ПФ; si,  - полюса ПФ.
- полюса ПФ.
Как видим, M(p) и N(p) – приведенные многочлены (коэффициент при старшем члене равен 1).
zj находятся как корни M(p)=0; W(p)=0
si - находятся как корни N(p)=0; W(p)= 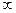
Если N и M не содержат общих множителей, то говорят, что zj и si - нули и полюса звена.
Определение: 1.Звено называется минимально-фазовым, если вещественные части всех его нулей и полюсов являются отрицательными или тождественно равными нулю.
2. Звено называется неминимально-фазовым, если оно содержит хотя бы один нуль или полюс с положительной вещественной частью.
Условие минимальной фазовости:
Re Si≤0,  , Re Zj≤0,
, Re Zj≤0, 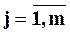
Неминимально-фазовые звенья, содержащие полюсы с положительной вещественной частью, называются неустойчивыми звеньями.
Пример. Рассмотрим апериодическое звено с ПФ:
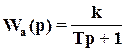 , Т>0
, Т>0
Следовательно, имеет полюс S1=-1/T <0 – минимально-фазовое звено.
Рассмотрим неустойчивое апериодическое звено с ПФ: 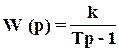 ;
;
S1=1/T >0 – неминимально-фазовое звено.
ЛАЧХ:
L(  )=La(
)=La(  );
);
L(  ) – неустойчивого, La(
) – неустойчивого, La(  ) – апериодического звеньев.
) – апериодического звеньев.
ФЧХ неустойчивого звена:
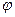 (
(  )=-[π+
)=-[π+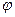 (
(  )],
)],
где
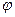 a(
a(  )= -arctg
)= -arctg  T (1)
T (1)
является ФЧХ апериодического звена.
Как видим,
|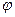 (
(  )|>|
)|>| 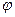 a(
a(  )|,
)|,  ,
,
кроме 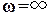 .
.

К минимально-фазовому звену из множества звеньев с одинаковыми ЛАЧХ, относится звено с ФЧХ (1)/
Выражение для ФЧХ минимально-фазового звена по теореме Бодэ
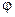 (
(  )=
)= , (*)
, (*)
где 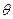 =lg
=lg  , а
, а 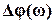 - малая величина.
- малая величина.
Из этого выражения следует, что для минимально-фазового звена:
1) можно найти 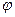 (
(  ) по L(
) по L(  );
);
2) выражение 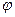 (
(  ) для ФЧХ при
) для ФЧХ при 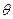 =lg
=lg  в основном определяется наклоном L(
в основном определяется наклоном L(  ), т.к.
), т.к. 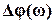 - малая величина.
- малая величина.
Условие минимальной фазовости позволяет находить W(p) по L(  ), и по W(p) находить
), и по W(p) находить 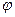 (
(  ), особенно просто по асимптотической ЛАЧХ.
), особенно просто по асимптотической ЛАЧХ.
Пример. Известна ЛАЧХ минимально-фазового звена. Надо найти W(p).
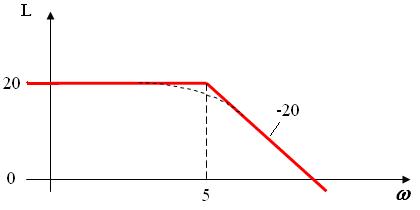
Так как 20lgk=20, следовательно, k=10;
1/T=5, поэтому T=0.2.
ПФ
W(p)=10/(0.2p+1),
т.к. звено минимально-фазовое. Отсюда ЛФЧХ
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 5526; Нарушение авторских прав?; Мы поможем в написании вашей работы!