Устойчивость систем автоматического управления

1) Понятие об устойчивости

Вопрос об устойчивости систем автоматического управления является основным в теории автоматического управления. Система автоматического управления состоит из объекта управления и управляющего устройства. Задачей управляющего устройства является поддержание системы в состоянии равновесия (т.е. в таком состоянии, при котором регулируемая величина – угол поворота, скорость, температура, напряжение и т.д. – сохраняет постоянное значение). Если система отклонилась от состояния равновесия (рабочей точки), то управляющее устройство вновь должно привести ее к этому состоянию. Поэтому проектирование системы начинается с определения тех состояний равновесия, которые система должна поддерживать.

Состояние равновесия нелинейной системы можно определить или аналитическим путем, решая нелинейное алгебраическое уравнение, соответствующее постоянству управляемой величины системы, или графоаналитическим путем, зная статические характеристики, связывающие выходные и входные величины всех элементов системы. Однако при таком определении всегда возникает вопрос: может ли физически существовать в системе найденное расчетным путем состояние равновесия? На простом примере легко показать, что найденные расчетным путем состояния равновесия не всегда могут существовать физически. Рассмотрим поверхность сложной формы, на которой находится шарик (рис. 1).

Рис. 1

Нужно найти положение равновесия шарика на этой поверхности. На шарик действует сила

,

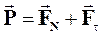состоящая из двух составляющих, одна из которых F_N уравновешивается реакцией со стороны поверхности, другая вызывает движение шарика вниз. Состояние равновесия будет иметь место, если =0, т.е. в точках А и В, где касательная к поверхности горизонтальна.

Таким образом, теоретический расчет дает два состояния равновесия для данной системы. Но если подойти к рассмотрению вопроса с практической стороны, то сразу видно, что в точке А шарик находиться не может. Поэтому состояние равновесия, соответствующее точке А, называется неустойчивым.

Состояние равновесия в точке В является устойчивым. Это означает, что данное состояние физически осуществимо в системе. Дадим более строгие определения устойчивого и неустойчивого состояний равновесия.

Для суждения об устойчивости состояния равновесия необходимо вывести систему из этого состояния путем приложения внешнего возмущения и наблюдать характер свободного движения системы после прекращения действия этого возмущения.

Состояние равновесия системы автоматического управления будет устойчивым, если после устранения возмущающего воздействия система с течением времени вновь возвращается к этому состоянию. Состояние равновесия системы является неустойчивым, если после устранения возмущающего воздействия система продолжает удаляться от состояния равновесия.

Таким образом, аналитическое рассмотрение вопроса о равновесии системы может привести к нахождению неустойчивого состояния равновесия. Поэтому всегда необходимо проверить, будет ли найденное состояние равновесия устойчивым. Это первая задача теории устойчивости.

Величина отклонения от состояния равновесия определяет «устойчивость в малом» и «устойчивость в большом». Если анализ устойчивости системы проводится при малых отклонениях от состояния равновесия, то говорят об «устойчивости в малом». Если же анализируется поведение системы при больших отклонениях от состояния равновесия, то говорят об «устойчивости в большом».

При анализе линеаризованных или линейных систем автоматического управления, являющихся линейной моделью реальных нелинейных систем, справедливой при малых отклонениях от состояния равновесия, рассматривается вопрос об «устойчивости в малом». Эта линейная модель приемлема лишь для конкретного состояния равновесия. Поэтому в случае анализа линейных систем, по существу, исследуется «устойчивость в малом» лишь одного определенного состояния равновесия нелинейной системы, которое может быть или устойчивым, или неустойчивым. Следовательно, по отношению к линейной системе удобнее говорить просто об ее устойчивости или неустойчивости, не затрагивая вопроса о состоянии равновесия. Рассмотрим условия устойчивости линейных систем.

2) Определение устойчивости линейной системы по виду корней характеристического уравнения

Поведение линейных систем описывается линейным дифференциальным уравнением. Поэтому исследование устойчивости таких систем сводится к исследованию линейного ДУ. Используя выражение для ПФ замкнутой системы

,

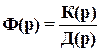уравнение движения системы в изображениях представим в виде

Д(р)y(р)=К(р)v(р) (1)

Так как анализ устойчивости производится после прекращения внешнего воздействия, т.е. при v=0, то ДУ свободного движения системы в изображениях будет иметь вид

Д(р)y(р)=0 (2)

или

.

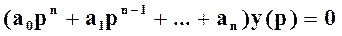Данное уравнение, записанное в обычной форме

(3)

представляет собой однородное уравнение с постоянными коэффициентами, а его общее решение y_cв(t) характеризует свободное движение системы, т.е. движение системы в отсутствие внешнего воздействия. Внешнее воздействие, которое действует на систему до начального момента t=0, влияет на ненулевые начальные условия (или их) порождает и от них (начальных условий) зависит свободное движение.

Если с течением времени свободное движение затухает, т.е. если

,

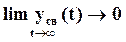то система будет устойчивая.

Если с течением времени свободное движение неограниченно возрастает, т.е. если

,

то такая система будет неустойчивая.

Наконец, в промежуточном случае, когда с течением времени y_cв(t) не возрастает неограниченно и не стремится к нулю, говорят, что система является предельно (критически) устойчивая (находится на границе устойчивости). Таким образом, устойчивость системы зависит от характера изменения y_cв(t) с ростом времени.

Решение однородного ДУ (3) можно представить (за исключением случая кратных корней) в виде

, (4)

где р₁, р₂,…, р_n – корни характеристического уравнения замкнутой системы Д(р)=0, а А₁, А₂,…,А_n – произвольные постоянные, зависящие от значения y_cв(t) и ее производных в начальный момент времени.

Величина y_cв(t) будет с течением времени стремиться к нулю только в том случае, если каждое слагаемое выражения (4) также будет стремиться к нулю.

Каждому вещественному корню р_к=-α_к в решении (4) будет соответствовать слагаемое

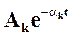. (5)

Если вещественный корень р_к = - α_к отрицателен, т.е. если α_к>0, то слагаемое вида (5) с течением времени будет стремиться к нулю. Если же вещественный корень р_к= - α_к положителен, т.е. α_к<0, то слагаемое (5) будет с течением времени возрастать. Каждой паре комплексно-сопряженных корней

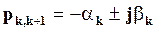
в выражении (5) будет соответствовать величина

,

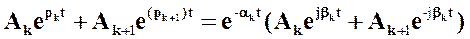которую с помощью формулы Эйлера можно привести к виду

(6),

Если вещественная часть комплексных корней отрицательна, т.е. если α_к > 0, то слагаемое вида (6) с течением времени будет затухать, так как амплитуда синусоиды будет стремиться к нулю. Если же вещественная часть комплексно-сопряженных корней положительна, т.е. α_к<0, то слагаемое (6) будет с течением времени возрастать, так как амплитуда синусоиды будет стремиться к бесконечности. Наконец, если вещественная часть комплексно-сопряженных корней будет равна 0, т.е. α_к=0, то при t→∞ слагаемое вида (5) не будет ни возрастать, ни стремиться к нулю.

Эти выводы остаются справедливыми, если среди корней характеристического уравнения замкнутой системы имеются кратные корни. Покажем, что это действительно имеет место. Каждой паре комплексно-сопряженных корней 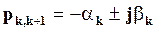кратности m в выражении (4) будет соответствовать величина

. (7)

Затухание данной колебательной составляющей определяется членом

(8)

Если вещественная часть кратных комплексно-сопряженных корней отрицательна, т.е. если α_к>0, то этот член стремится к нулю и система устойчива, так как по правилу Лопиталя

.

Если же вещественная часть кратных комплексно-сопряженных корней положительна, т.е. α_к<0, то этот член, а следовательно, и вся величина (8) будет стремиться к бесконечности.

Если вещественная часть кратных комплексно-сопряженных полюсов равна нулюилиимеют место кратные нулевые вещественные корни, т.е. α_к=0, то легко показать, используя (7), что в этом случае соответствующие этим корням слагаемые в выражении (4) будут неограниченно возрастать.

На основании рассмотрения выражений (5) 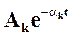, (6) и (7) можно сделать следующие выводы:

1. Линейная замкнутая система автоматического управления устойчивая, если все корни ее характеристического уравнения Д(р)=0 отрицательны или имеют отрицательную вещественную часть (рис. 2а, в), т.е.

.

Рис. 2

2. Линейная замкнутая система автоматического управления неустойчива я, если хотя бы один из корней ее характеристического уравнения Д(р)=0 имеет положительную вещественную часть или имеются кратные корни с нулевой вещественной частью (рис. 2б, г).

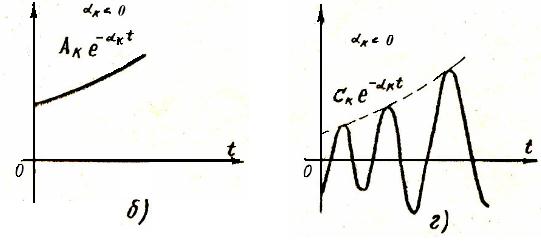
Рис. 2

3. Линейная замкнутая система автоматического управления предельно (критически, маргинально) устойчивая, если вещественная часть комплексно-сопряженных корней ее характеристического уравнения Д(р)=0 равна нулю или один вещественный корень равен нулю, а все остальные корни имеют отрицательные вещественные части и нет кратных корней с нулевой вещественной частью (рис. 2д).

Рис. 2

Дата добавления: 2014-01-07