Геометрическая интерпретация условий устойчивости

Лекция 15

Корни характеристического уравнения удобно изображать в виде точек на комплексной плоскости, по осям которой откладываются действительные и мнимые части этих корней (рис. 3). Такая плоскость называется плоскостью корней. Если вещественная часть какого-либо корня отрицательная, то точка, изображающая этот корень, будет лежать слева от мнимой оси. Следовательно, для того, чтобы линейная система автоматического управления была устойчивой, необходимо и достаточно, чтобы все корни ее характеристического уравнения Д(р)=0 располагались в плоскости корней

слева от мнимой оси, т.е. были левыми.

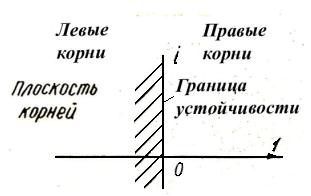
Рис. 3

При изменении параметров системы корни, перемещаясь в комплексной плоскости, могут перейти из левой половины плоскости в правую, т.е. стать правыми, что будет свидетельствовать о превращении устойчивой системы в неустойчивую. Следовательно, линейная система будет неустойчивой, если хотя бы один корень ее характеристического уравнения является правым или, по крайней мере, один кратный нулевой корень или кратные комплексно-сопряженные корни расположены на мнимой оси.

Таким образом, мнимая ось является как бы границей, разделяющей плоскость корней на две области, одна из которых соответствует устойчивости системы, другая – неустойчивости.

Говорят, что линейная система находится на границе устойчивости или критически устойчивая, если пара комплексно-сопряженных корней (колебательная граница устойчивости) или один действительный корень (апериодическая граница устойчивости) лежат на мнимой оси, а все остальные корни располагаются слева от этой оси и нет кратных корней, расположенных на мнимой оси.

На рисунке ниже показано, каким образом можно оценить устойчивость линейной замкнутой системы по расположению корней ее характеристического уравнения на комплексной плокости p_k (плоскости корней характеристического уравнения).

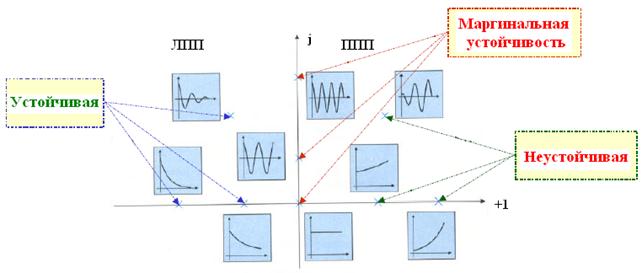
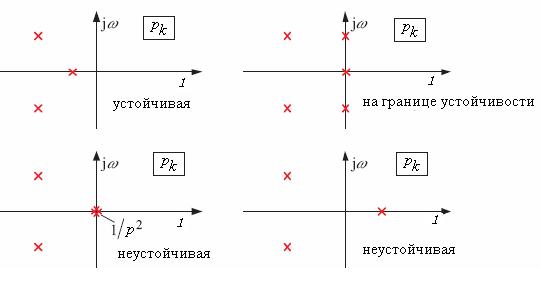
Заметим, что корни характеристического уравнения имеют другое название, а именно полюсы системы или полюсы передаточной функции системы. Поэтому все вышеприведенные выводы, касающиеся устойчивости системы, остаются в силе, если мы заменим в них слова «корни характеристического уравнения» на слова «полюсы системы».

Дата добавления: 2014-01-07