Теоремы Ляпунова об устойчивости по линейному приближению

При исследовании систем автоматического регулирования возникает вопрос о справедливости суждения об устойчивости нелинейной системы по ее линеаризованным уравнениям или, как еще говорят, по уравнениям первого приближения. Обоснование законности такой линеаризации содержится в теоремах русского ученого (1892г.), основоположника теории устойчивости А.М. Ляпунова, которые мы приведем без доказательства:

Теорема 1. Если все корни характеристического уравнения линеаризованной системы имеют отрицательные вещественные части, то исходная система, описываемая нелинейными уравнениями, будет устойчивой.

Теорема 2. Если среди корней характеристического уравнения линеаризованной системы имеется хотя бы один корень с положительной вещественной частью, то исходная нелинейная система будет неустойчивой.

Теорема 3. При наличии нулевых и чисто мнимых корней поведение исходной нелинейной системы не может быть определено по линеаризованным уравнениям и необходимо проводить дополнительное исследование для решения вопроса об ее устойчивости.

Эти теоремы относятся к случаю «устойчивости в малом».

Таким образом, если характеристическое уравнение решено и корни его известны, то легко судить о том, устойчива система или нет. Однако вычисление корней просто произвести только для уравнений первой и второй степени. Общие выражения для корней уравнений 3-й и 4-й степени известны, но очень громоздки и практически мало удобны. Уравнения более высоких степеней вообще не имеют общих выражений, и решение их связано с очень большими трудностями.

Поэтому в теории автоматического регулирования были разработаны правила, которые позволяют судить об устойчивости системы, минуя вычисление корней. Эти правила называются критериямиустойчивости. С помощью критериев устойчивости можно не только судить об устойчивости системы, но и выяснить влияние тех или иных параметров и элементов схемы на устойчивость.

Рассмотрим несколько критериев устойчивости.

3. Критерий устойчивости Гурвица

Для того чтобы судить об устойчивости, нужно определить, имеет ли характеристическое уравнение корни с положительной вещественной частью. О наличии корней с положительной вещественной частью можно судить по коэффициентам характеристического уравнения. Правила, по которым можно определить, имеет ли система корни с положительной вещественной частью, были сформулированы независимо друг от друга английским математиком Раусом (1887) и швейцарским математиком Гурвицем (1895) и получили название критериев Рауса и Гурвица.

Приведем без доказательства формулировку критерия Гурвица.

Пусть дано характеристическое уравнение замкнутой системы

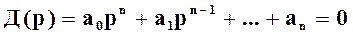
Для суждения об устойчивости системы по критерию Гурвица их коэффициентов этого уравнения составляется определитель порядка n, называемый главным определителем Гурвица.

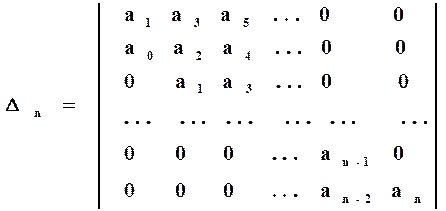
Главный определитель Гурвица образуется следующим образом. По главной диагонали выписываются коэффициенты уравнения, начиная со второго (а₁) и до последнего (а_n) включительно. Столбцы вверх от главной диагонали заполняются коэффициентами по возрастающим индексам, а столбцы вниз - коэффициентами по убывающим индексам. Остающиеся пустые места заполняются нулями.

Критерий Гурвица гласит: система устойчива, если а₀ и все определители 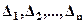положительны, причем

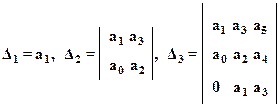и т.д.

Т.е. если а₀ >0, .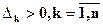

Нетрудно убедиться, что все эти определители образуются из главного определителя Гурвица путем последовательного вычеркивания столбцов и строк.

Если главный определитель 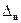равен нулю, то система находится на границе устойчивости. Так как 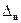= а₀ 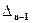, то это возможно в двух случаях:

1) a_n=0,

2) 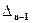=0,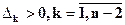

В первом случае говорят об апериодической границе устойчивости, во втором – о колебательной границе устойчивости.

Заметим, что характеристический многочлен , все нули р_к которого имеют отрицательную вещественную часть, называется гурвицевым многочленом. Следовательно, для устойчивости системы необходимо и достаточно, чтобы характеристический многочлен замкнутой системы был гурвицевым.

Пример. Пусть дано уравнение третьего порядка

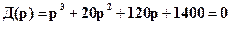
Найдем определители Гурвица:

.

Так как а₀=1>0, >0, >0, >0, то система устойчивая.

4. Критерий устойчивости Михайлова

Этот критерий был предложен советским ученым А.В.Михайловым в 1938 году. В основе его лежит понятие годографа характеристического многочлена (или годографа характеристического уравнения).

Рассмотрим характеристический многочлен замкнутой системы

. (8)

Заменяя в (8) р на jw, получим

.

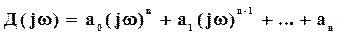При каждом значении w величина 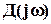будет представлять собой вектор на комплексной плоскости. При изменении w от -∞ до ∞ конец этого вектора опишет кривую, называемую годографом характеристического уравнения. Критерий Михайлова позволяет судить об устойчивости системы по виду годографа характеристического уравнения.

Рассмотрим на примере способ построения годографа характеристического уравнения. Пусть имеется характеристический многочлен

Д(р)=р²+2р+5.

Подставляя в это выражение вместо р значение jw получим

Д(jw)=5 - w ² + j2w =A(w)+jB(w),

где A(w)=5 - w² – вещественная часть годографа; B(w)=2w – мнимая часть годографа.

Сам годограф легко построить по точкам (рис. 4), задаваясь несколькими значениями w в пределах от - ∞ до + ∞.

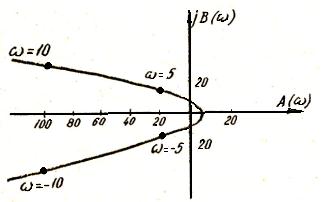
Рис. 4

Данные для построения приведены в таблице (A(w)=5 - w², B(w)=2w):

w	A A(w)	B(w)
±1 ±5 ±10	-20 -95	±2 ±10 ±20

Около каждой точки годографа указывают значение частоты. Как видим, при замене w на – w получается комплексно-сопряженное значение для годографа. Это не случайно. Выражение Д(р) аналогично выражению для передаточной функции W(p) и переход от Д(р) к Д(jw) производится так же, как и переход от передаточной функции W(p) к амплитудно-фазовой характеристике W(jw). Следовательно, и свойства выражения Д(jw) аналогичны свойствам АФХ. В частности, при замене w на –w мы приходим к комплексно-сопряженному выражению

Д(-jw)=Д*(jw). (8a)

Поэтому во многих случаях можно ограничиться рассмотрением только одной ветви годографа, соответствующей положительным значениям w. Для получения критерия устойчивости Михайлова представим годограф Д(jw) в ином виде. Обозначим через р₁, р₂, …, р_n корни характеристического уравнения Д(р)=0. Тогда характеристический многочлен можно представить в виде

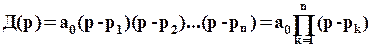. (9)

Заменяя р на jw, получим следующее выражение для годографа:

.

Рассмотрим какое-то значение w=w₁. Обозначим через argД(jw) угол, который составит вектор Д(jw) с вещественной осью при w=w₁, т.е.

a=argД(jw₁) (10)

при w=w₁.

Это иллюстрируется на рис. 5.

Рис. 5

Поставим задачу определить, насколько изменится аргумент Д(jw) при изменении w от -∞ до +∞, т.е. найдем величину

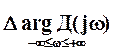
Так как Д(jw) представляется в виде произведения отдельных сомножителей, а аргумент произведения равен сумме аргументов сомножителей, то при а₀ > 0 изменение аргумента Д(jw) равно сумме изменений аргументов сомножителей

(11)

Вид отдельных сомножителей Д(jw) определяется значением корней р_к характеристического уравнения. Здесь могут быть два случая:

а) Вещественная часть корня р_к отрицательна, т.е. Re p_k<0;

б) Вещественная часть корня р_к положительна, т.е. Re p_k>0.

Изобразим сомножители выражения (9) в виде векторов на комплексной плоскости и определим изменение их аргумента, считая поворот вектора против часовой стрелки положительным (рис. 6).

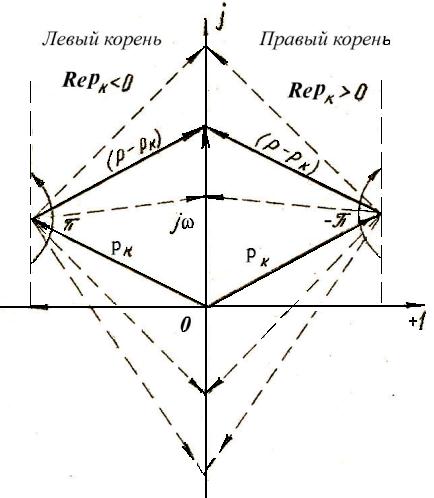
Рис. 6

Из этого рисунка непосредственно видно, что

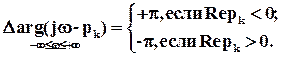(12)

Предположим, что характеристическое уравнение имеет q корней с положительной вещественной частью, а значит n - q корней с отрицательной вещественной частью. При этом в соответствии с выражениями (11) и 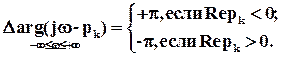(12) изменение аргумента равно:

.

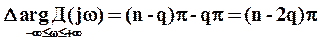Учитывая симметрию годографа Д(jw), выражаемую соотношением (8,а), можем ограничиться рассмотрением диапазона изменения w от 0 до ∞. При этом изменение аргумента будет в два раза меньше:

.

Если число корней с положительной вещественной частью равно нулю, т.е. q=0, то

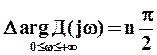. (13)

Это соотношение и выражает критерий Михайлова, который может быть сформулирован следующим образом: Система автоматического управления устойчива, если при возрастании w от 0 до ∞, вектор Д(jw) повернется на угол 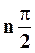против часовой стрелки, где n – степень характеристического уравнения системы, или, что то же самое, если годограф характеристического уравнения при изменении w от 0 до ∞ обходит последовательно n квадратов комплексной плоскости, начиная с положительной действительной оси, нигде не обращаясь в нуль.

На рис. 8 приведены годографы устойчивых (а) и неустойчивых (б) систем для некоторых значений n.

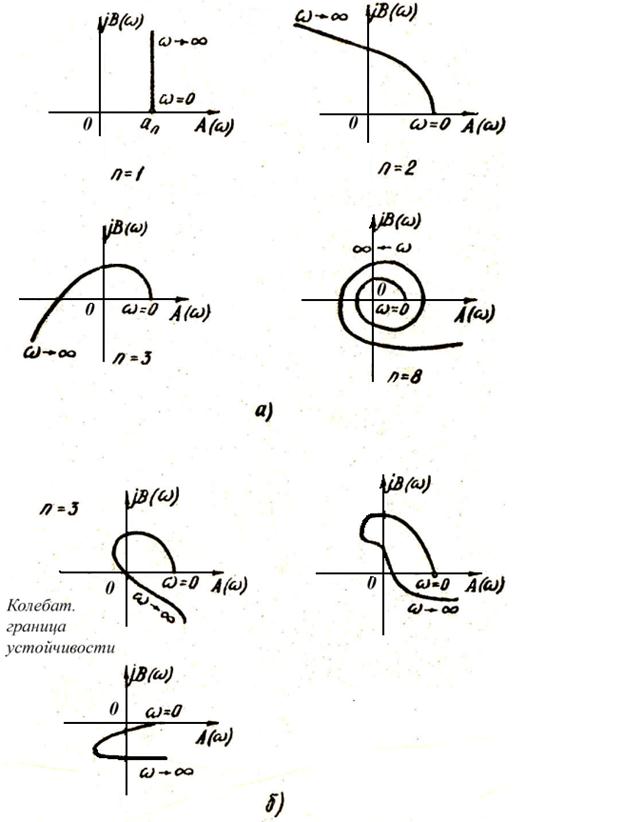
Рис. 8

Заметим, что критерий Михайлова можно использовать также для определения устойчивости разомкнутой системы. При этом необходимо строить годограф характеристического уравнения разомкнутой системы D(jw), получаемый из характеристического многочлена разомкнутой системы D(p) путем замены р на jw.

Дата добавления: 2014-01-07