Относительная устойчивость

Лекция 18

Рассмотренный на прошлой лекции критерий Найквиста позволяет определить устойчивость, строго говоря, абсолютную устойчивость замкнутой системы. Однако «просто» устойчивости системы еще недостаточно для ее работоспособности. Есть две причины, которые заставляют ввести понятие относительной устойчивости. Первая причина заключается в том, что система, кроме всего прочего, должна иметь приемлемые временные характеристики. Вторая причина кроется в том, что система должна быть робастной, т.е. должна сохранять свои свойства при неопределенности и изменчивости модели, используемой для определения устойчивости. Модель системы никогда не является точной. Следовательно, использование модели может показать, что система является устойчивой, тогда как на самом деле реальная система окажется неустойчивой. К понятию относительной устойчивости приходим следующим образом.

Если амплитудно-фазовая характеристика разомкнутой системы пересекает критическую точку (-1,j0), то замкнутая система находится на колебательной границе устойчивости, по сути дела, является неустойчивой. При этом в системе спустя некоторое время после включения наблюдаются незатухающие колебания. Чем дальше проходит АФХ системы справа от критической точки, то очевидно меньше ее (системы) колебательность, т.е. менее колебательной является ее реакция, или, как говорят, больше ее относительная устойчивость. О степени относительной устойчивости, другими словами, о степени удаленности АФХ разомкнутой системы относительно критической точки принято судить с помощью так называемых запасов устойчивости.

Запас устойчивости по амплитуде (модулю) характеризует расстояние между критической точкой (-1,j0) и ближайшими точками пересечения характеристики W(jw) с вещественной осью.

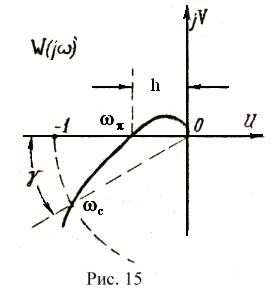
Если точка пересечения располагается справа от критической точки, то в качестве запаса устойчивости по амплитуде принимают величину 1/h, обратную расстоянию h от этой точки пересечения до начала координат (рис. 15), где h =R (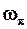)=| W(j 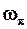) |. Здесь 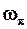частота, при которой АФХ разомкнутой системы пересекает отрицательную вещественную ось, другими словами, частота, при которой ФЧХ системы достигает значения, равного 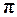, т.е.

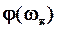=arg W(j )= =-.

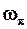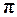Запас устойчивости по амплитуде определяется как число, на которое должен быть умножен коэффициент усиления разомкнутой системы, чтобы замкнутая система оказалась на границе устойчивости. Таким образом, если коэффициент усиления устойчивой системы равен k и запас устойчивости определяется значением 1/h, то критический коэффициент усиления k_кр находится как

k_кр = k*1/h.

Одного запаса устойчивости по амплитуде недостаточно, чтобы судить о степени устойчивости системы. Действительно, запас устойчивости может быть достаточно большим, даже бесконечным, однако АФХ разомкнутой системы может проходить в непосредственной близости от критической точки. Поэтому

вводится еще один запас устойчивости.

Запас устойчивости по фазе определяется следующим образом. На комплексной плоскости U, jV проводится окружность единичного радиуса с центром в начале координат (рис. 15) и отмечается точка ее пересечения с характеристикой W(jw). Угол γ, образуемый проходящим через эту точку радиусом (лучом) и отрицательной частью вещественной оси, называется запасом устойчивости по фазе. Так как частота, при которой АФХ пересекает окружность единичного радиуса, есть частота среза , то формально можно определить запас устойчивости по фазе как

,

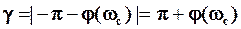где 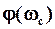есть значение фазо-частотной характеристики разомкнутой системы при частоте среза. Физически запас по фазе определяется наименьшей величиной угла, на который надо повернуть АФХ, чтобы замкнутая система оказалась на границе устойчивости.

Величина 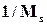, где 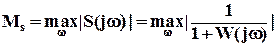определяет наименьшее расстояние от АФХ разомкнутой системы до критической точки ( - 1,j0).

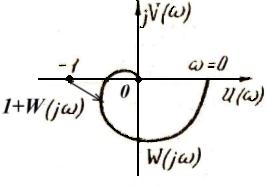
Рекомендуемое значение лежит между 1.2 и 2.

Для того чтобы определить запасы устойчивости по логарифмическим частотным характеристикам, рассмотрим вид логарифмических частотных характеристик, соответствующих устойчивой и неустойчивой системам.

7. Логарифмический критерий устойчивости

Для проверки устойчивости замкнутой системы можно использовать также логарифмические частотные характеристики разомкнутой системы (диаграммы Боде). Рассмотрим вначале ситуацию, когда каждая из логарифмических частотных характеристик лишь один раз пересекает ось частот и разомкнутая система является устойчивой.

1) Замкнутая система неустойчива

Для неустойчивой системы, которая устойчива в разомкнутом состоянии, АФХ W(jw) приведена на рис. 16,a. Мы видим, что в данном случае значению фазы φ( 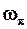)= -180^о (- радиан) соответствует значение R( 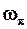) больше единицы, так что при этом L( 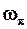)=20lgR( 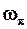)>0.

Рис. 16

Это является признаком неустойчивой замкнутой системы и соответствует взаимному расположению логарифмических частотных характеристик L(w) и φ(w), показанному на рис. 16, б.

Для удобства отсчета фазы ось абсцисс при построении логарифмической фазовой характеристики обычно проводят при значении φ(w)=-180^о (- радиан).

2) Замкнутая система устойчивая

Из рассмотрения АФХ W(jw) устойчивой разомкнутой системы, которая в замкнутом состоянии устойчивая, видим, что значению φ( )=-180^о (- радиан) соответствует R( )=h <1 (рис. 18,а). При этом

L( 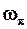)=20lgR( )=20lgh<0

(рис. 18,б), что является признаком устойчивой замкнутой системы.

Рис. 17

Ордината 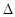L=-20lgh характеристики L(w), соответствующая значению φ( 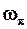)= - 180^о (- радиан), определяет запас устойчивости по амплитуде, выраженный в децибелах. Рекомендуется иметь запасы устойчивости:

от 12 дБ до 20 дБ для задающего воздействия

от 3. 5 дБ до 9. 5 дБ для возмущающего воздействия

=

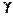от 4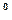0 до 60 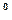для задающего воздействия

от 20 до 50 для возмущающего воздействия.

Угол γ, представляющий собой запас устойчивости по фазе, определяется точкой В, полученной в результате пересечения характеристикой W(jw) окружности единичного радиуса, проведенной из начала координат. Следовательно, в точке В величина R( 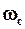)=1, а это значит, что частота, соответствующая точке В, есть частота среза .

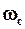Таким образом, на логарифмических характеристиках угол γ представляет собой значение фазовой частотной характеристики, соответствующее частоте среза w_c (рис. 17б).

Замкнутая система будет находиться на колебательной границе устойчивости, если на той же частоте w_с, где ЛАЧХ разомкнутой системы обращается в нуль, значение фазовой частотной характеристики равно -180 градусов (-радиан).

Вывод. Если каждая из характеристик L(w) и φ(w) устойчивой в разомкнутом состоянии системы лишь один раз пересекает ось частот, то для устойчивости замкнутой системы необходимо и достаточно, чтобы выполнялось условие

w_с<.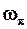

Если w_с=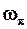=, то система находится на границе устойчивости.

Общий случай. Будем считать «+1 – пересечением» логарифмической фазовой частотной характеристикой уровня -180 градусов (-радиан) снизу вверх и «-1 – пересечением» - пересечение логарифмической фазовой частотной характеристикой уровня -180 градусов (-радиан) сверху вниз при положительном значении логарифмической амплитудно-частотной характеристикой.

Логарифмический критерий устойчивости гласит:

1. Если разомкнутая система имеет l правых полюсов, то для устойчивости замкнутой системы необходимо и достаточно, чтобы на интервале частот, когда L(w)>0, общее число пересечений логарифмической фазовой частотной характеристикой уровня -180 градусов снизу вверх превышало общее число пересечений сверху вниз на l/2.

На рис. 18 показаны АФХ и соответствующие ей логарифмические характеристики.

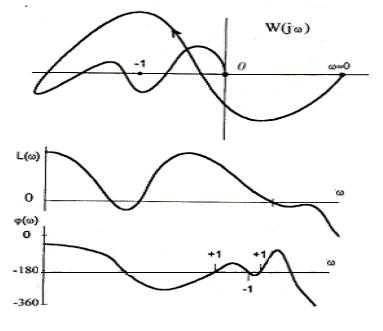
Рис. 18

Как видим, число пересечений снизу вверх (+1) равно 2, а число пересечений сверху вниз (-1) равно 1. Отсюда замкнутая система устойчивая, если разомкнутая система имеет l=2 правых полюсов.

2. Если разомкнутая система устойчивая, то для устойчивости замкнутой системы необходимо и достаточно, чтобы на интервале частот, когда L(w)>0, общее число пересечений логарифмической фазовой частотной характеристикой уровня -180 градусов снизу вверх было равно общему числу пересечений сверху вниз.

8. Устойчивость систем управления с запаздыванием

В предыдущих разделах критерий устойчивости Найквиста рассматривался применительно к системам, передаточные функции которых имели дробно-рациональный вид. Однако во многих системах управления присутствует запаздывание по времени, существенно влияющее на устойчивость. Запаздывание по времени – это промежуток времени между моментом, когда в каком-то месте системы произойдет некоторое событие, и моментом, когда это событие проявит себя в другом месте. Критерий Найквиста обладает тем преимуществом, что он позволяет учесть влияние этого запаздывания на устойчивость системы. Идеальное запаздывание по времени можно охарактеризовать передаточной функцией

W_d(p)=e^-pτ,

где τ есть время запаздывания. Критерий Найквиста остается в силе и для систем с запаздыванием, поскольку множитель e^-pτ не приводит к появлению дополнительных полюсов или нулей в передаточной функции разомкнутой системы. Этот множитель, не влияя на амплитудную характеристику систему, вносит только дополнительный отрицательный фазовый сдвиг.

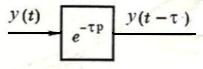
Рис. 19

Подобное запаздывание свойственно системам, в которых имеет место перемещение материалов, когда между точкой, где произошло како-то изменение переменной, и точкой, где проявляется соответствующий эффект, проходит определенное (конечное) время.

В качестве примера приведем систему управления прокатом стальной полосы, изображенную на рис. 20. Электродвигатель управляет расстоянием между валками таким образом, чтобы минимизировать ошибку в толщине полосы. Если скорость движения полосы равна v, то запаздывание между точкой изменения скорости валков и точкой измерения толщины полосы равно

.

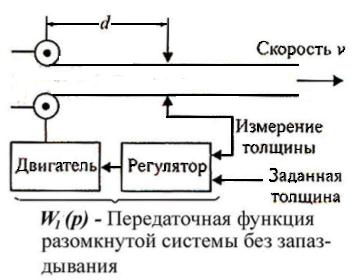
Рис.20

Таким образом, для уменьшения запаздывания необходимо уменьшать расстояние от валков до точки измерения толщины полосы. Но, так или иначе, влияние запаздывания полностью исключить невозможно, поэтому передаточную функцию разомкнутой системы управления надо рассматривать в виде

W(p)=W₁ (p)e ^{– pτ}.

При этом АФХ разомкнутой системы с запаздыванием приобретает вид

W(jw)=W₁ (jw)e ^{– j wt}.

Обычно мы исследуем устойчивость замкнутой системы, построив годограф W(jw) на комплексной плоскости и исследуя его положение относительно точки -1. Аналогично, мы можем построить логарифмические частотные характеристики и исследовать их вид в окрестности точки с координатами 0 дБ и -180^о. Множитель e ^–jwt приводит к дополнительному фазовому сдвигу

φ(w) = - wτ, (*)

который должен быть добавлен к фазовому сдвигу, создаваемому функцией

W₁ (jw). (Обратите внимание, что выражение (*) определяет угол в радианах.) Следующий пример иллюстрирует, как просто учесть запаздывание при анализе устойчивости с помощью построения АФХ W(jw) (Рис.21)

Рис. 21

Для разомкнутой системы с запаздыванием, описываемой передаточной функцией W₁(p)e^-pτ, нужно построить АФХ. Разомкнутая система имеет АФХ W (jw)=W₁(jw) e ^{– j wt} и, следовательно,

|W₁(jw) e ^{– j wt} | =| W₁ (jw)| и arg [W₁ (jw) e ^{– j wt}] =arg W₁ (jw) - wτ.

Как видим, АФХ системы с запаздыванием будет отличаться от АФХ системы без запаздывания (разумеется, речь идет о разомкнутых системах) лишь тем, что к argW₁(jw) должен быть добавлен угол – wτ. Этот угол измеряется в радианах и увеличивается с ростом частоты. Результирующая АФХ W(jw) изображена на рис. 22 вместе с годографом для W₁(jw)), который показан пунктирной линией.

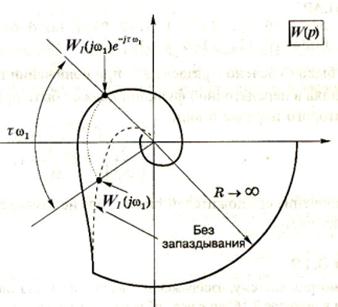
Рис.22

Мы видим, что единственный эффект запаздывания состоит в том, что он добавляет в систему отставание по фазе. Разумеется, это ухудшает устойчивость системы, поскольку АФХ поворачивается в сторону точки -1.

В ряде случаев необходимо определить максимально допустимую величину запаздывания τ_кр, при которой замкнутая система еще остается устойчивой. Для этого достаточно найти максимальный угол, на который можно повернуть АФХ W₁(jw) системы без запаздывания (τ=0) и чтобы при этом она (АФХ) не охватила точку -1.

Рис. 23

Этот угол (рис. 23), очевидно, соответствует запасу устойчивости по фазе системы без запаздывания. Отсюда

.

Следовательно,

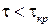- замкнутая система устойчива,

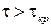- замкнутая система неустойчива.

Критерий устойчивости: если АФХ устойчивой разомкнутой системы с запаздыванием не охватывает точку (-1, j0), то замкнутая система с запаздыванием является устойчивой.

Дата добавления: 2014-01-07