Лекция 16. 5. Критерий устойчивости Найквиста

5. Критерий устойчивости Найквиста

Этот критерий был первоначально разработан в 1932 году Найквистом для исследования устойчивости усилителей с отрицательной обратной связью. В 1938 году советский ученый А.В.Михайлов, обратив внимание на общность основного принципа действия усилителей с обратной связью и систем автоматического управления, применил этот метод в теории автоматического управления.

Сущность критерия Найквиста в том, что он позволяет по виду АФХ разомкнутой системы судить об устойчивости замкнутой системы. При этом АФХ разомкнутой системы может быть или получена расчетным путем из выражения для передаточной функции, или снята экспериментально.

Пусть передаточная функция разомкнутой системы

,

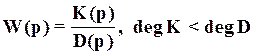так что АФХ равна

.

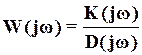Рассмотрим новую функцию f(jw), связанную с соотношением

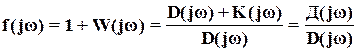. (14)

Здесь 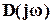представляет собой годограф характеристического уравнения разомкнутой системы, а Д(jw) – замкнутой системы.

Критерий устойчивости рассмотрим для нескольких случаев.

a) Разомкнутая система устойчива.

Устойчивость разомкнутой системы можно установить без всяких вычислений по структурной схеме системы. Так, например, разомкнутая система, состоящая из устойчивых звеньев и не содержащая обратных связей, всегда устойчива. Если имеются звенья, содержащие обратную связь, то эти звенья надо исследовать особо.

Если разомкнутая система устойчива, то на основании критерия Михайлова изменение аргумента 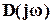будет равно

,

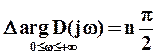где n – степень характеристического уравнения разомкнутой системы, совпадающая со степенью характеристического многочлена замкнутой системы Д(р)=D(р)+К(р), т.к. для строго физически осуществимых систем степень К(р) меньше степени D(р).

Изменение аргумента Д(jw) в общем случае равно

,

где q – число корней характеристического уравнения Д(р)=0, лежащих в правой части комплексной плоскости, т.е. число правых корней.

Изменение аргумента f(jw) равно разности изменений аргументов числителя Д(jw) и знаменателя D(jw), т.е.

.

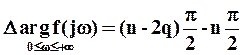Замкнутая система устойчива, если q=0, т.е. когда

.

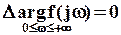Если представить годограф f(jw) на комплексной плоскости (рис. 9), то нетрудно установить, что вектор f(jw) при изменении w от 0 до ∞ опишет на комплексной плоскости угол, равный нулю, лишь в том случае, если годограф f(jw) не охватывает начала координат. В этом случае замкнутая система устойчива.

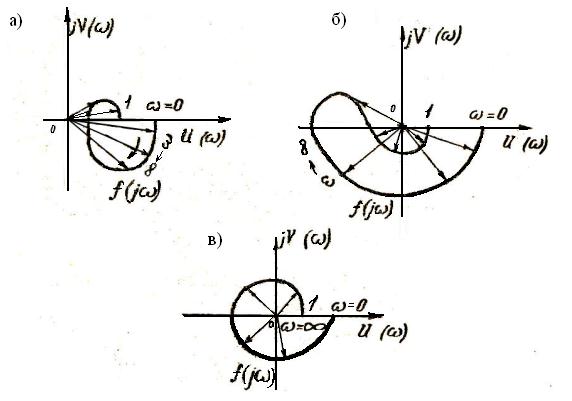
Рис. 9

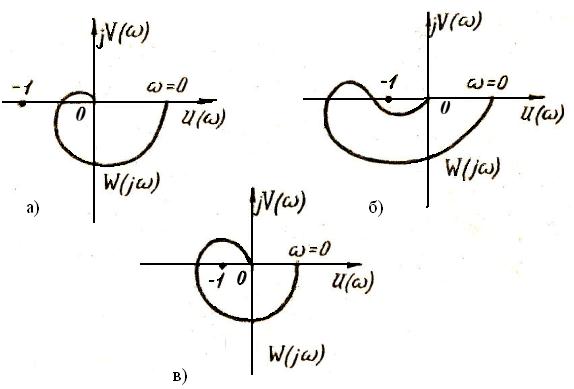
Рис. 10

От годографа f(jw) нетрудно перейти к АФХ разомкнутой системы (рис. 10).

W(jw)=f(jw) - 1,

которая представляет собой ту же кривую 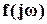, но сдвинутую на единицу влево. При этом изменение аргумента 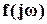при изменении w от 0 до ∞ будет равно нулю, если АФХ разомкнутой системы не охватывает точку (-1,j0) (рис. 10).

Следовательно, если разомкнутая система устойчива, то замкнутая система будет также устойчива, при условии, что АФХ разомкнутой системы не охватывает точку (-1, j0).

Особо следует выделить случай, когда АФХ проходит через точку (-1, j0) и поэтому находится на колебательной границе устойчивости. Такому положению АФХ соответствует критический, или предельный коэффициент усиления k_кр.

Применительно к диаграмме Найквиста этот критерий звучит так: если разомкнутая система устойчива, то замкнутая система будет также устойчива, при условии, что диаграмма Найквиста не охватывает точку

(-1, j0) ( Рис. 10.1 ).

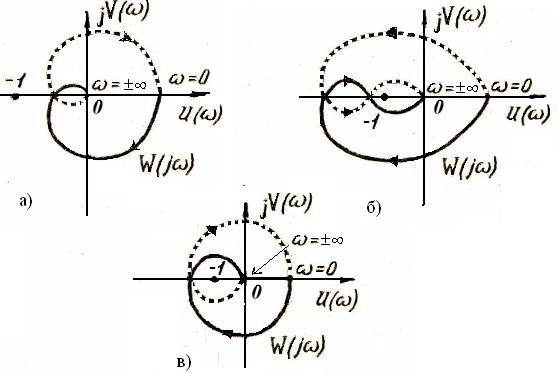
Рис. 10.1

б) Разомкнутая система неустойчива.

Такой случай может встретиться при рассмотрении систем, содержащих неустойчивые звенья или неустойчивые замкнутые контуры.

Пусть характеристическое уравнение разомкнутой системы D(р) имеет l корней в правой полуплоскости.

Тогда изменение аргумента D(jw) будет равно:

.

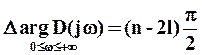Если замкнутая система устойчива, то

.

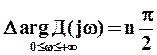При этом в соответствии с тем, изменение аргумента f(jw) равно разности изменений аргументов числителя Д(jw) и знаменателя D(jw)

.

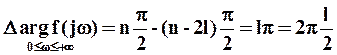Следовательно, кривая 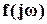при изменении w от 0 до ∞ должна охватывать начало координат l/2 раз, а АФХ разомкнутой системы должна охватывать точку с координатами (-1,j0) l/2 раз.

Вывод. Если разомкнутая система является неустойчивой, то замкнутая система будет устойчивой при условии, что АФХ разомкнутой системы охватывает точку с координатами (-1,j0) l/2 раз в положительном направлении, где l – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости (правых корней).

На рис. 11 приведена АФХ W(jw) устойчивой системы для случая, когда характеристическое уравнение разомкнутой системы имеет два корня с положительной вещественной частью (l=2).

Применительно к диаграмме Найквиста этот критерий звучит так: Если разомкнутая система является неустойчивой, то замкнутая система будет устойчивой при условии, что диаграмма Найквиста охватывает точку с координатами (-1,j0) l раз в положительном направлении, где l – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости (правых корней).

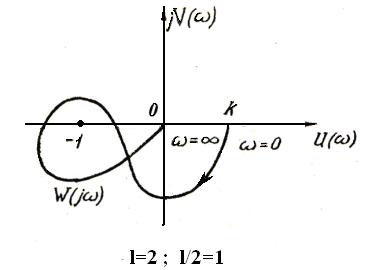
Рис. 11

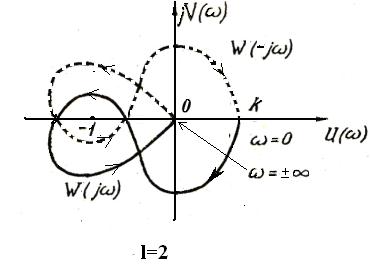
Рис. 11.1

На рис. 11.1 приведена диаграмма Найквиста устойчивой системы для случая, когда характеристическое уравнение разомкнутой системы имеет два корня с положительной вещественной частью (l =2).

в) Разомкнутая система нейтрально-устойчивая

Система называется нейтрольно-устойчивой, если ее характеристическое уравнение содержит нулевые корни и левые корни, т.е. характеристическое уравнение имеет вид

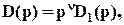
где 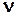=1,2,3,…, а уравнение 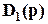=0 включает лишь левые корни.

АФХ нейтрально устойчивой разомкнутой нейтрольно-устойчивой системы начинается в бесконечности, т.е. характеристика не является замкнутой, что затрудняет применение критерия Найквиста. Чтобы распространить критерий Найквиста на этот случай, необходимо подробнее исследовать, как ведет себя АФХ при w→0, т.е. в бесконечности. АФХ разомкнутой системы получается из передаточной функции 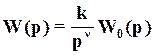при р=jw для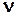=1,2,3,…. Изобразим р на комплексной плоскости (рис. 12).

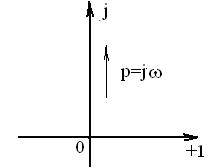
Рис. 12

При изменении w от 0 до ∞ функция р=jw меняется вдоль мнимой оси от 0 до + j∞. При w=0 р находится в начале координат (р=0), благодаря чему выражение для передаточной функции обращается в бесконечность, что затрудняет исследование АФХ. Это затруднение можно обойти следующим приемом. Рассмотрим некоторый другой закон изменения р такой, чтобы при р≠0 имело место р=jw, но при р→0 начало координат было исключено, как, например, показано на рис. 13.

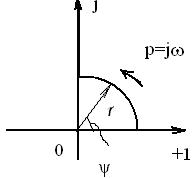
Рис. 13

Следовательно, при всех конечных р (р≠0) имеем обычную АФХ

.

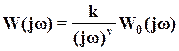Однако при р→0 закон изменения р другой:

р=rе^jψ,

причем r→0, а ψ меняется от 0 до π/2.

Следовательно, при р→0

.

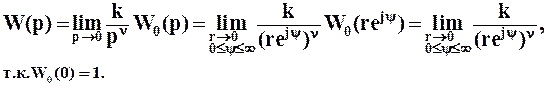При таком законе изменения р мы получим обычный вид АФХ для всех конечных значений w, т.к. р=jw, и мы можем исследовать вид АФХ при р→0, т.е. в бесконечности.

Учитывая, что при р→0, r→0, а ψ меняется от 0 до π/2, получим

W(р)= Rе ^–jνψ,

где R = ∞, а νψ меняется от 0 до νπ/2.

Следовательно, при р→0, а значит при w →0, АФХ представляет собой дугу бесконечно большого радиуса, который описывает угол от 0 до νπ/2 в отрицательном направлении (дополнение). Например, при ν =1 имеем νπ/2= π/2. Из рис. 14 видно, что характеристика получилась замкнутой и к ней можно применить критерий Найквиста.

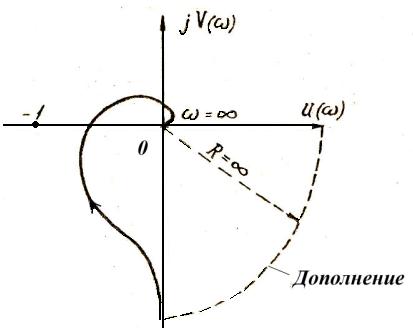
Рис. 14

Следовательно, если разомкнутая система нейтральноустойчивая, то замкнутая система будет устойчивая, при условии, что АФХ разомкнутой системы, дополненная дугой бесконечно большого радиуса в ν четвертей окружности, не охватывает точку (-1, j0), где ν число нулевых корней характеристического уравнения разомкнутой системы D(p)=0 (число интеграторов) или при условии, что диаграмма Найквиста разомкнутой системы, дополненная дугой бесконечно большого радиуса в 2ν четвертей окружности, не охватывает точку (-1, j0) ( рис. 14.1 ).

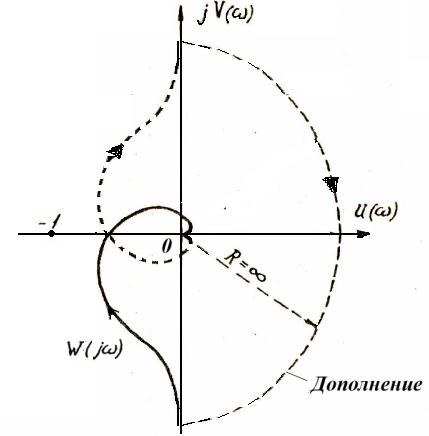
Рис. 14.1

Дата добавления: 2014-01-07