Внутренняя устойчивость системы управления

Лекция 19

Определение устойчивости системы с использование лишь знаменателя передаточной функции замкнутой системы по задающему воздействию

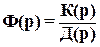
как характеристического многочлена системы может привести к ошибочному результату, если при вычислении передаточной функции разомкнутой системы имеет место сокращение правых нулей/полюсов. В противном случае можно лишь говорить о внешней устойчивости системы или об устойчивости типа вход-выход. Дело в том, что при этом ряд других передаточных функций системы содержат правые полюсы, другими словами, нули своих знаменателей,

что говорит о неустойчивости этих передаточных функций и, следовательно, о внутренней неустойчивости системы. Понятие внутренней устойчивости может поставить в тупик некоторых студентов в связи с тем, что в большинстве учебников по управлению устойчивость замкнутой системы оценивается по корням характеристического уравнения. Следующий пример используется для иллюстрации такого случая.

Пример. Пусть передаточные функции объекта и обратной связи:

.

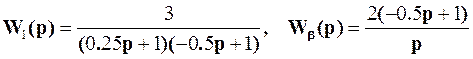Тогда передаточная функция разомкнутой системы оказывается равной

W(p)=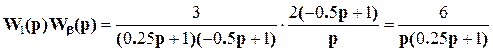

и характеристическое уравнение замкнутой системы имеет вид

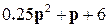=0,

что говорит об устойчивости замкнутой системы, т.к. корни этого уравнения являются левыми.

Однако, передаточные функции замкнутой системы по задающему воздействию

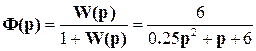
и по возмущению

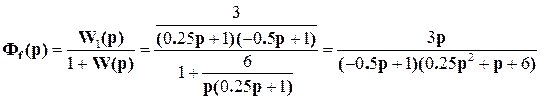
имеют разные знаменатели, причем последняя передаточная функция имеет правый полюс, равный 2 (корень уравнения 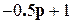=0), что говорит о

неустойчивости этой передаточной функции и о внутренней неустойчивости замкнутой системы.

Определение. Замкнутая система называется внутренне устойчивой, если все ее передаточные функции Ф(p), 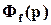, , 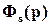связывающие выход y с внешними воздействиями, и все ее передаточные функции Ф_uv(p)=u(p)/v(p), Ф_uf(p)=u(p)/f(p), Ф_us(p)=u(p)/s(p), связывающие управление u с внешними воздействиями, являются устойчивыми передаточными функциями. Разумеется, что данное определение справедливо лишь по отношению к системе с одной степенью свободы. Однако его легко обобщить и на систему с двумя степенями свободы.

Физически внутренняя устойчивость означает, что при ненулевых начальных условиях все переменные системы [ y(t), 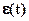,u(t),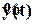] с течением времени стремятся к нулю.

Опустить

11. Робастная устойчивость

Если модель системы точно не определена (обычный случай), то необходимо обеспечить, по меньшей мере, номинальную устойчивость. Все, что было до сих пор сказано об устойчивости, основано на предположении, что линеаризованная модель объекта точно описывает систему в окрестности состояния равновесия. Так как все реальные системы являются нелинейными, то удобно рассматривать саму линейную аппроксимацию (линеаризованную модель) системы как обладающую модельной неопределенностью, так что модель, которую мы приняли для исследования устойчивости, является лишь номинальной моделью объекта. Все методы анализа устойчивости, прямые или косвенные, при использовании номинальной модели гарантируют только номинальную устойчивость.

Робастная устойчивость имеет отношение к устойчивости для всех моделей в рамках (пределах) модельной неопределенности. Робастная устойчивость может быть в принципе гарантирована, если условия устойчивости соблюдаются для всех возможных моделей неточно определенной системы. К сожалению, при этом анализ устойчивости оказывается весьма затруднительным. Однако критерий Найквиста может быть использован для суждения о робастной устойчивости, если ввести в рассмотрение модельную неопределенность как частотную фун кцию (модельную неопределенность в частотной области), которая оценивает уровень модельной неопределенности для каждого значения частоты. В общем случае, как показала практика, неопределенность имеет тенденцию быть больше на высоких частотах и модуль АФХ разомкнутой системы может быть измерен точнее, чем ее аргумент (фаза).

С помощью критерия Найквиста можно определить робастную устойчивость. Число охватов критической точки (-1, j0) АФХ разомкнутой системы (диаграммой Найквиста) является решающим тестом в частотной области для ответа на вопрос о номинальной устойчивости. Если число охватов удовлетворяет условию номинальной устойчивости, расстояние от АФХ разомкнутой системы до критической точки (-1,j0) определяет робастную устойчивость в терминах модельной неопределенности в частотной области. Это расстояние |1+W(jw)| (см. рисунок ниже) обратно

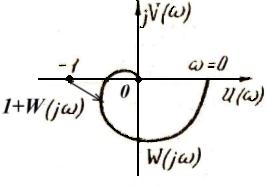
пропорционально модулю |S(jw)| так называемой функции чувствительности

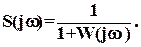
Таким образом, малая чувствительность на данной частоте соответствует большему расстоянию от АФХ разомкнутой системы до критической точки

( - 1,j0) и отсюда высокой робастной устойчивости на этой частоте.

Величина

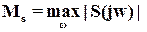
является мерой робастной устойчивости. Величина 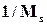определяет наименьшее расстояние от АФХ разомкнутой системы до критической точки ( - 1,j0). Рекомендуемое значение лежит между 1.2 и 2.

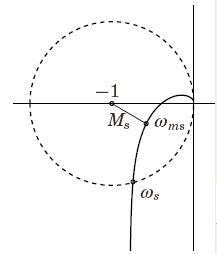
Запас устойчивости по модулю является мерой робастной устойчивости для частоты w_π, на которой ФЧХ разомкнутой системы равна -180 градусам. Этот запас есть количественная оценка робастной устойчивости при «чистом» отклонении (возмущении) модуля АФХ разомкнутой системы. В то время как запас устойчивости по фазе является количественной мерой робастной устойчивости для частот (они называются частотами среза w _с), на которых модуль АФХ разомкнутой системы принимает значения, равные единице. Этот запас есть количественная оценка робастной устойчивости при «чистом» отклонении (возмущении) фазы АФХ разомкнутой системы. Заметим, что замкнутая система с модулем АФХ (со значениями АЧХ), превышающим единицу в некотором диапазоне частот, имеет ограниченный запас устойчивости по фазе, что вытекает из критерия Найквиста. Никогда не забывайте, что расстояние от АФХ разомкнутой системы до критической точки (-1,j0) неуместно для использования, если число охватов не удовлетворяет критерию Найквиста, т.е. если номинальная устойчивость не имеет места. Вот почему непродуманное использование управляющего устройства с высоким коэффициентом усиления не может служить как жизнеспособная стратегия управления.

Дата добавления: 2014-01-07