Понятие о корневом годографе

Читать

За рубежом широко используется подход к анализу и синтезу систем управления, связанный с применением так называемого корневого годографа (КГ). Чтобы ввести понятие о корневом годографе рассмотрим структуру Блэка

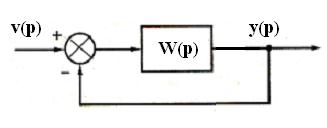
Пусть передаточная функция разомкнутой системы представлена в приведенном виде

,

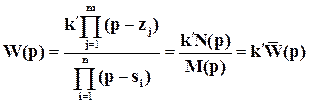где z_j -нули, s_i – полюсы, 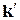-приведенный коэффициент усиления разомкнутой системы, n >m. При этом передаточная функция замкнутой системы

,

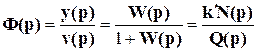где знаменатель

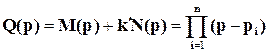
называется характеристическим многочленом и корни p_i характеристического уравнения

Q(p) = 1+ 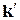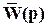==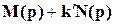 0

называются полюсами замкнутой системы.

Полюсы замкнутой системы (корни характеристического уравнения замкнутой системы), очевидно, являются функциями 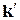при заданных N(p) и M(p), т.е. p_i =f_i (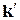), i=1,2,…,n.

Определение. Корневым годографом называется геометрическое место полюсов замкнутой системы на комплексной плоскости при изменении приведенного коэффициента усиления разомкнутой системы 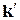от 0 до .

Для систем невысокого порядка можно построить корневой годограф «вручную».

Пример. W(p)=k/p² . При этом

Ф(p)=.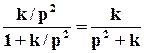

Отсюда

Q(p)= 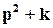, p² =k, p_1,2 = j.

Какой вид имеет диаграмма полюсов замкнутой системы зависит от k= 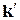. Мы можем составить таблицу

Как выглядит параметризованная диаграмма нулей и полюсов?

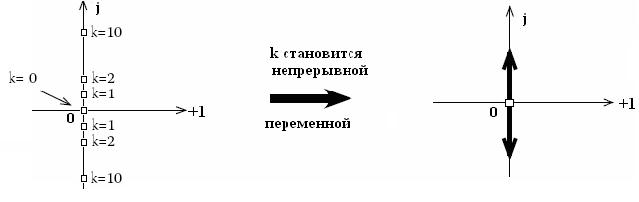
Здесь - полюсы замкнутой системы p_1,2.

Заметим, что при построении корневых годографов принято обозначать как 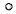- нули и как - полюсы разомкнутой системы.

В общем случае вручную корневой годограф построить трудно и требуются инструменты MATLAB rlocus(num,den) или sisotool, чтобы получить точные его очертания. Однако мы можем представить общую конфигурацию корневого годографа, используя несколько правил его построения. Все эти правила извлекаются из уравнений

1+ 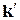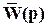= 0,

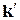
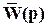=-1.

Эти уравнения удовлетворяются при выполнении двух условий (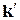>0):

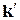
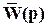1. ||=1условие (уравнение) для модуля,

2. arg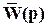=(12r)180⁰ , r=0,1,… 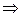условие (уравнение) для фаз.

Удивительно, что большое число правил может быть получено из этих простых условий.

Правило 1: Число ветвей корневого годографа, которые являются траекториями полюсов замкнутой системы, равно числу полюсов разомкнутой системы. Другими словами, замыкание разомкнутой системы не изменяет число полюсов.

Правило 2: Ветви годографа начинаются в полюсах разомкнутой системы и m из них заканчиваются в нулях разомкнутой системы, остальные n-m уходят в бесконечность.

Правило 3: Участки вещественной оси принадлежат корневому годографу, если справа от них расположено нечетное число вещественных нулей и полюсов. Комплексно-сопряженные нули и полюсы не оказывают влияния на принадлежность участков вещественной оси корневому годографу.

Уравнение (условие) фаз:

arg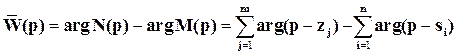=(12r)180⁰ .

Из характеристического уравнения

Q(p) = 1+ 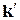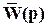==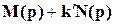 0

с вещественными коэффициентами следует, что комплексные полюсы замкнутой системы являются сопряженными и отсюда КГ является симметричным относительно вещественной оси.

Правило 4: Если ветвь корневого годографа расположена на вещественной оси между парой полюсов, то на этой ветви должна быть точка разветвления (отделения) КГ. Аналогично, если ветвь корневого годографа расположена на вещественной оси между парой нулей, то на этой ветви должна быть точка входа двух ветвей КГ.

Примеры.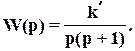

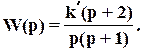
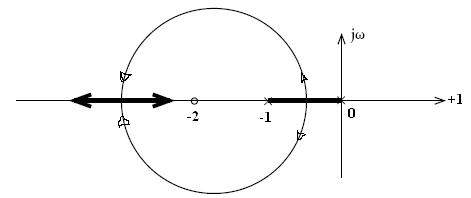
Правило 5: Если 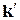становится достаточно большим, то n-m ветвей КГ уходят в бесконечность. Эти ветви приближаются к асимптотам, составляющим углы к вещественной оси

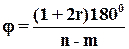, r=0,1,…,n-m-1.

Центр звезды этих асимптот лежит на вещественной оси в точке с абсциссой

.

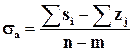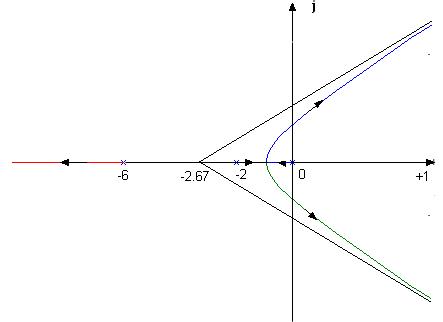
Пример.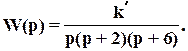

Правило 1: 3 ветви,

Правило 2: ветви начинаются в точках 0, -2, -6 и все уходят в бесконечность,

Правило 3: участки на вещественной оси расположены между 0 и -2, между

-6 и -.

Правило 4: точка разветвления КГ расположена между 0 и -2,

Правило 5: -асимптоты 60⁰ , 180⁰ и 300⁰ = -60⁰

- центр звезды в .

Дата добавления: 2014-01-07