Оценка времени переходного процесса

Время переходного процесса определяется как время, в течение которого переходная составляющая затухает до величины 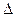% от своего начального значения. Поэтому для оценки времени переходного процесса необходимо рассмотреть скорость затухания мод системы.

Выражение (87) 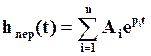включает в себя как апериодические составляющие (моды) 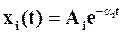, соответствующие вещественным полюсам , так и колебательные составляющие (моды) , соответствующие комплексно-сопряженным полюсам 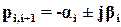. Затухание этих составляющих определяется множителем 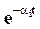. При этом чем больше вещественная часть 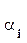полюса р_i (или сам вещественный полюс), тем быстрее затухает мода.

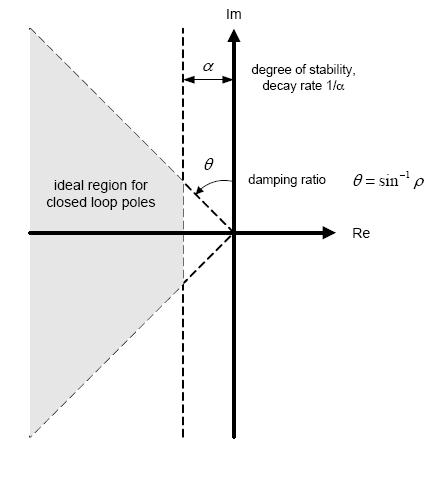
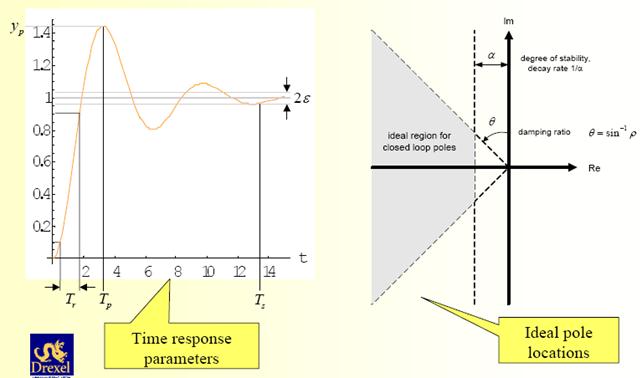
Корни характеристического уравнения (полюса замкнутой системы) удобно изображать в виде точек на комплексной плоскости (рис. 19), по осям которой отложены вещественная и мнимая части корней. Так как можно говорить только о качестве переходного процесса устойчивой системы, у которой вещественные части всех корней отрицательны, то все корни будут расположены слева от мнимой оси. При этом, чем дальше от мнимой оси расположены корни и 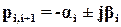, тем большему значению 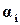они соответствуют.

Наиболее медленно будет затухать мода 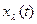, имеющая наименьшее 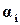. Поэтому можно приближенно считать, что скорость затухания переходного процесса определяется такой модой 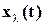, которая соответствует корням наиболее близко расположенным к мнимой оси. Величина 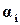, наименьшая из всех значений 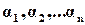, являющихся вещественными частями корней характеристического уравнения Д(р)=0, называется степенью устойчивости и обозначается 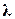(рис. 19).

Эта величина позволяет приближенно оценить время переходного процесса при 5% -допустимой ошибке

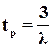. (89)

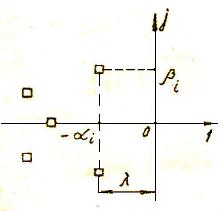
Рис. 19

Оценка перерегулирования.

Перерегулирование системы зависит от поведения колебательных составляющих

,

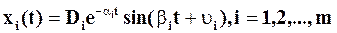так как колебательные процессы в системе будут наблюдаться только в том случае, когда характеристическое уравнение содержит комплексно-сопряженные корни 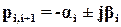. Склонность системы к колебаниям характеризует оценка

,

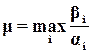которую называют колебательностью или степенью колебательности.

Таким образом, чем больше величина 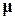, тем более колебательный характер будут иметь переходные процессы и наоборот. В пределе при 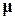=∞ полюса системы будут «чисто» мнимыми, и в ней будут наблюдаться переходные процессы в виде незатухающих колебаний. В случае, когда 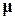=0, все корни характеристического уравнения будут вещественными, и в системе будут возникать апериодические процессы. Для системы второго порядка установлена взаимосвязь между колебательностью и перерегулированием в виде соотношения

.

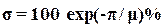Отметим, что при 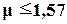значение перерегулирования в системе составит .

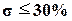Связь колебательности и относительного коэффициента затухания для системы второго порядка определяется формулой

.

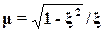Рассмотренные корневые методы оценки не учитывают влияние на постоянные коэффициенты А_i других нулей и полюсов замкнутой системы, наличие которых, как это видно из выражений (87) и (87а), может существенно изменить качество переходного процесса.

Анализируя выражения (87) и (87а), можно сделать следующие выводы относительно влияния расположения нулей и полюсов на вид и характер переходной характеристики.

1) Основное влияние на качество переходного процесса оказывает группа ближайших к мнимой оси нулей и полюсов (так называемых доминирующих нулей и полюсов).

2) Длительность переходного процесса в основном определяется степенью устойчивости системы, равной абсолютному значению вещественной части ближайших к мнимой оси комплексных полюсов замкнутой системы или вещественного полюса, если он является ближайшим к мнимой оси. При этом длительность переходного процесса может быть определена по формуле (89) .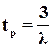

3) Величина перерегулирования 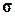зависит от степени колебательности 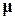доминирующих комплексных полюсов и от степени близости к мнимой оси остальных нулей и полюсов замкнутой системы.

4) Близкие к мнимой оси нули увеличивают перерегулирование, а близкие (но не доминирующие) полюсы его уменьшают.

Не останавливаясь на доказательстве всех этих пунктов, приведем лишь соображения, подтверждающие вывод об увеличении перерегулирования при введении в систему нулей.

Пусть САУ описывается в отсутствии нулей передаточной функцией Ф₀(р). Введем в эту систему левый нуль z= -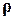, так чтобы при этом не изменился коэффициент усиления замкнутой системы k_з=Ф(0). Тогда передаточная функция примет вид

.

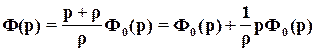По изображению

найдем переходную характеристику полученной системы

,

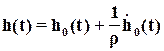как сумму переходной характеристики 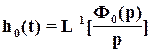исходной и взвешенной производной этой характеристики.

В начале переходного процесса характеристика h(t) возрастает с большой скоростью и поэтому ее производная 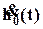положительна и имеет большую величину (рис. 24). В результате сложения кривых h₀(t) и 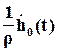получается кривая h(t), имеющая большее перерегулирование, причем перерегулирование увеличивается тем значительнее, чем меньше абсолютное значение 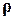нуля передаточной функции Ф(р).

Введение большего числа нулей приводит к тому же эффекту.

Рис. 24

Для системы второго порядка с комплексно-сопряженными полюсами с ПФ

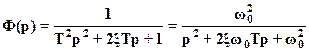
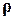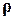
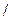
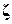
введение левого нуля z = -увеличивает перерегулирование при а= 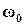< 4.

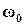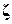Переходная характеристика и логарифмические ЧХ замкнутой системы для =1 и =0.5, 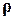=0.25, 0.5, 1, 2, 5 и 10 изображены на рис. ниже.

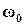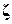Переходная характеристика и логарифмические ЧХ для =1 и =0.5, 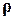=-0.25, -0.5, -1, -2, -5 и -10 (неминимально-фазовая система с правым нулем z=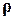) изображены на рис. ниже. В этом случае имеет место недорегулирование, определяемое величиной отрицательного максимума переходной характеристики.

Инструмент ICTOOLS

Дата добавления: 2014-01-07